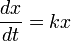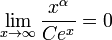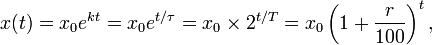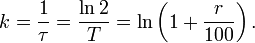Exponential growth
In mathematics, exponential growth (or geometric growth) occurs when the growth rate of a function is always proportional to the function's current size. Such growth is said to follow an exponential law (but see also Malthusian growth model). This implies for any exponentially growing quantity, the larger the quantity gets, the faster it grows. But it also implies that the relationship between the size of the dependent variable and its rate of growth is governed by a strict law, of the simplest kind: direct proportion. It is proved in calculus that this law requires that the quantity is given by the exponential function, if we use the correct time scale. This explains the name.
Contents |
[edit] Intuition
The phrase exponential growth is often used in nontechnical contexts to mean merely surprisingly fast growth. In a strictly mathematical sense, though, exponential growth has a precise meaning and does not necessarily mean that growth will happen quickly. In fact, a population can grow exponentially but at a very slow absolute rate (as when money in a bank account earns a very low interest rate, for instance), and can grow surprisingly fast without growing exponentially. And some functions, such as the logistic function, approximate exponential growth over only part of their range. The "technical details" section below explains exactly what is required for a function to exhibit true exponential growth.
But the general principle behind exponential growth is that the larger a number gets, the faster it grows. Any exponentially growing number will eventually grow larger than any other number which grows at only a constant rate for the same amount of time (and will also grow larger than any function which grows only subexponentially). This is demonstrated by the classic riddle in which a child is offered two choices for an increasing weekly allowance: the first option begins at 1 cent and doubles each week, while the second option begins at $1 and increases by $1 each week. Although the second option, growing at a constant rate of $1/week, pays more in the short run, the first option eventually grows much larger:
| Week | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Option 1 | 1c | 2c | 4c | 8c | 16c | 32c | 64c | $1.28 | $2.56 | $5.12 | $10.24 | $20.48 | $40.96 | $81.92 | $163.84 | $327.68 |
| Option 2 | $1 | $2 | $3 | $4 | $5 | $6 | $7 | $8 | $9 | $10 | $11 | $12 | $13 | $14 | $15 | $16 |
We can describe these cases mathematically. In the first case, the allowance at week n is 2n cents; thus, at week 15 the payout is 215 = 32768c = $327.68. All formulas of the form kn, where k is an unchanging number greater than 1 (e.g., 2), and n is the amount of time elapsed, grow exponentially. In the second case, the payout at week n is simply n + 1 dollars. The payout grows at a constant rate of $1 per week.
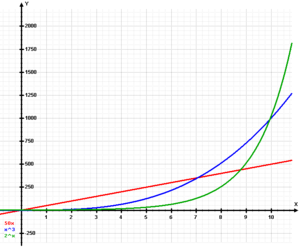
This image shows a slightly more complicated example of an exponential function overtaking subexponential functions:
The red line represents 50x, similar to option 2 in the above example, except increasing by 50 a week instead of 1. Its value is largest until x gets around 7. The blue line represents the polynomial x3. Polynomials grow subexponentially, since the exponent (3 in this case) stays constant while the base (x) changes. This function is larger than the other two when x is between about 7 and 9. Then the exponential function 2x (in green) takes over and becomes larger than the other two functions for all x greater than about 10.
Anything that grows by the same percentage every year (or every month, day, hour etc.) is growing exponentially. For example, if the average number of offspring of each individual (or couple) in a population remains constant, the rate of growth is proportional to the number of individuals. Such an exponentially growing population grows three times as fast when there are six million individuals as it does when there are two million. Bank accounts with fixed-rate compound interest grow exponentially provided there are no deposits, withdrawals or service charges. Mathematically, the bank account balance for an account starting with s dollars, earning an annual interest rate r and left untouched for n years can be calculated as s(1 + r)n. So, in an account starting with $1 and earning 5% annually, the account will have 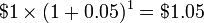 after 1 year,
after 1 year, 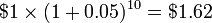 after 10 years, and $131.50 after 100 years. Since the starting balance and rate do not change, the quantity (1 + 0.05) = 1.05 can work as the value k in the formula kn given earlier.
after 10 years, and $131.50 after 100 years. Since the starting balance and rate do not change, the quantity (1 + 0.05) = 1.05 can work as the value k in the formula kn given earlier.
[edit] Technical details
Let x be a quantity growing exponentially with respect to time t. By definition, the rate of change dx/dt obeys the differential equation:
where k ≠ 0 is the constant of proportionality (the average number of offspring per individual in the case of the population). (See logistic function for a simple correction of this growth model where k is not constant). The solution to this equation is the exponential function 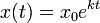 -- hence the name exponential growth ('e' being a mathematical constant). The constant
-- hence the name exponential growth ('e' being a mathematical constant). The constant 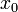 is the initial size of the population.
is the initial size of the population.
In the long run, exponential growth of any kind will overtake linear growth of any kind (the basis of the Malthusian catastrophe) as well as any polynomial growth, i.e., for all α:
There is a whole hierarchy of conceivable growth rates that are slower than exponential and faster than linear (in the long run). Growth rates may also be faster than exponential. The linear and exponential models are merely simple candidates but are those of greatest occurrence in nature.
In the above differential equation, if k < 0, then the quantity experiences exponential decay.
[edit] Characteristic quantities of exponential growth
The law of exponential growth can be written in different but mathematically equivalent forms, by using a different base. The most common forms are the following:
where as in the example above x0 expresses the initial quantity (i.e. x(t) for t = 0).
The quantity k is called the growth constant; the quantity r is known as the growth rate (percent increase per unit time); τ is the e-folding time; and T is the doubling time. Indicating one of these four equivalent quantities automatically permits calculating the three others, which are connected by the following equation (which can be derived by taking the natural logarithm of the above):
A popular approximated method for calculating the doubling time from the growth rate is the rule of 70,
i.e. 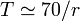 (or better:
(or better: 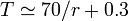 ).
).
[edit] Limitations of exponential models
As discussed above, an important point about exponential growth is that even when it seems slow on the short run, it becomes impressively fast on the long run, with the initial quantity doubling at the doubling time, then doubling again and again. For instance, a population growth rate of 2% per year may seem small, but it actually implies doubling after 35 years, doubling again after another 35 years (i.e. becoming 4 times the initial population), etc. This implies that both the observed quantity and its time derivative will become several orders of magnitude larger than what was initially meant by the person who conceived the growth model. Because of this, some effects not initially taken into account will distort the growth law, usually moderating it as for instance in the logistic law. Exponential growth of a quantity placed in the real world (i.e. not in the abstract world of mathematics) is a model valid for a temporary period of time only.
For this reason, some people challenge the exponential growth model on the ground that it is valid for the short term only, i.e. nothing can grow indefinitely. For instance, a population in a closed environment cannot continue growing if it eats up all the available food and resources; industry cannot continue pumping carbon from the underground into the atmosphere beyond the limits connected with oil reservoirs and the consequences of climate change; etc. Problems of this kind exist for every mathematical representation of the real world, but are specially felt for exponential growth, since with this model growth accelerates as variables increase in a positive feedback, to a point were human response time to inconvenients can be insufficient (on these points, see also the Exponential stories below).
[edit] Examples of exponential growth
- Biology.
- Microorganisms in a culture dish will grow exponentially, at first, after the first microorganism appears (but then logistically until the available food is exhausted, when growth stops).
- A virus (SARS, West Nile, smallpox) of sufficient infectivity (k > 0) will spread exponentially at first, if no artificial immunization is available. Each infected person can infect multiple new people.
- Human population, if the number of births and deaths per person per year were to remain at current levels (but also see logistic growth).
- Many responses of living beings to stimuli, including human perception, are logarithmic responses, which are the inverse of exponential responses; the loudness and frequency of sound are perceived logarithmically, even with very faint stimulus, within the limits of perception. This is the reason that exponentially increasing the brightness of visual stimuli is perceived by humans as a smooth (linear) increase, rather than an exponential increase. This has survival value. Generally it is important for the organisms to respond to stimuli in a wide range of levels, from very low levels, to very high levels, while the accuracy of the estimation of differences at high levels of stimulus is much less important for survival.
- Computer technology
- Processing power of computers. See also Moore's law and technological singularity (under exponential growth, there are no singularities. The singularity here is a metaphor.).
- In computational complexity theory, computer algorithms of exponential complexity require an exponentially increasing amount of resources (e.g. time, computer memory) for only a constant increase in problem size. So for an algorithm of time complexity 2^x, if a problem of size x=10 requires 10 seconds to complete, then a problem of size x=11 will require 20 seconds, and x=12 will require 40 seconds. This kind of algorithm typically becomes unusable at very small problem sizes, often between 30 and 100 items (most computer algorithms need to be able to solve much larger problems, up to tens of thousands or even millions of items in reasonable times, something that would be physically impossible with an exponential algorithm). Also, the effects of Moore's Law do not help the situation much because doubling processor speed merely allows you to increase the problem size by one. E.g. if a slow processor can solve problems of size x in time t, then a processor twice as fast could only solve problems of size x+1 in the same time t. So exponentially complex algorithms are most often impractical, and the search for more efficient algorithms is one of the central goals of computer science.
- Internet traffic growth.
- Investment. The effect of compound interest over many years has a substantial effect on savings and a person's ability to retire. See also rule of 72
- Physics
- Avalanche breakdown within a dielectric material. A free electron becomes sufficiently accelerated by an externally applied electrical field that it frees up additional electrons as it collides with atoms or molecules of the dielectric media. These secondary electrons also are accelerated, creating larger numbers of free electrons. The resulting exponential growth of electrons and ions may rapidly lead to complete dielectric breakdown of the material.
- Nuclear chain reaction (the concept behind nuclear weapons). Each uranium nucleus that undergoes fission produces multiple neutrons, each of which can be absorbed by adjacent uranium atoms, causing them to fission in turn. If the probability of neutron absorption exceeds the probability of neutron escape (a function of the shape and mass of the uranium), k > 0 and so the production rate of neutrons and induced uranium fissions increases exponentially, in an uncontrolled reaction.
- Exponential increases appear in each level of a starting member's downline as each subsequent member recruits more people.
[edit] External links
- Exponent calculator - One of the best ways to see how exponents work is to simply try different examples. This calculator enables you to enter an exponent and a base number and see the result.
[edit] References
- Meadows, Donella H., Dennis L. Meadows, Jørgen Randers, and William W. Behrens III. (1972) The Limits to Growth. New York: University Books. ISBN 0-87663-165-0
- Porritt, J. Capitalism as if the world matters, Earthscan 2005. ISBN 1-84407-192-8
- Thomson, David G. Blueprint to a Billion: 7 Essentials to Achieve Exponential Growth, Wiley Dec 2005, ISBN 0-471-74747-5
- Tsirel, S. V. 2004. On the Possible Reasons for the Hyperexponential Growth of the Earth Population. Mathematical Modeling of Social and Economic Dynamics / Ed. by M. G. Dmitriev and A. P. Petrov, pp. 367–9. Moscow: Russian State Social University, 2004.
| |
Some content on this page may previously have appeared on Citizendium. |