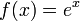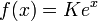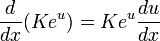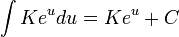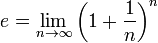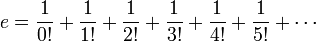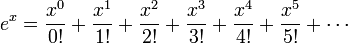e (mathematics)
e is a constant real number equal to 2.71828 18284 59045 23536.... Irrational and transcendental, e is the base of the natural logarithms. The exponential function (the inverse to the natural logarithm)
is equal to its derivative, i.e. 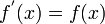 . For this reason, the exponential function plays a central role in analysis.
. For this reason, the exponential function plays a central role in analysis.
e is sometimes called "Euler's number" in honor of the Swiss mathematician Leonhard Euler who studied it and demonstrated its mathematical importance. Equally, it is sometimes called "Napier's constant" in honor of the Scottish mathematician John Napier who introduced logarithms.
Contents |
[edit] Properties
In 1737, Leonhard Euler proved that e is an irrational number[1], i.e. it cannot be expressed as a fraction, only as an infinite continued fraction. In 1873, Charles Hermite proved it was a transcendental number[1], i.e. it is not a root of any polynomial with rational coefficients.
e is the base of the natural logarithms. The exponential function
for K constant, is equal to its derivative, i.e. 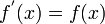 . For any differentiable function u, we have
. For any differentiable function u, we have
for K constant; also,
for K and C constants. The solutions of many differential equations are based on those properties.
[edit] History
There is no precise date for the discovery of this number[2]. In 1624, Henry Briggs, one of the first to publish a logarithm table, gives its logarithm, but does not formally identify e. In 1661, Christiaan Huygens remarks the match between the area under the hyperbola and logarithmic functions. In 1683, Jakob Bernoulli studies the limit of 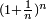 , but nobody links that limit to natural logarithms. Finally, in a letter sent to Huyghens, Gottfried Leibniz sets e as the base of natural logarithm (even if he names it b).[3]
, but nobody links that limit to natural logarithms. Finally, in a letter sent to Huyghens, Gottfried Leibniz sets e as the base of natural logarithm (even if he names it b).[3]
[edit] Definitions
There are many ways to define e. The most common are probably
and
[edit] References
- ↑ 1.0 1.1 Eli Maor, e: The Story of a Number, Princeton University Press, 1994, p.37. ISBN 0-691-05854-7.
- ↑ John J. O'Connor et Edmund F. Robertson, The number e, MacTutor History of Mathematics archive. Consulted 2008-01-10.
- ↑ Eli Maor, e: The Story of a Number, Princeton University Press, 1994. ISBN 0-691-05854-7.
- ↑ This equation is a special case of the Taylor series for the exponential function:
| |
Some content on this page may previously have appeared on Citizendium. |