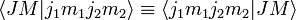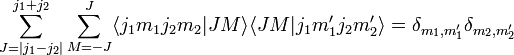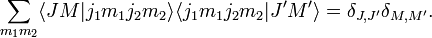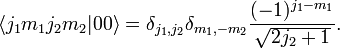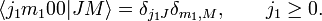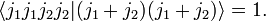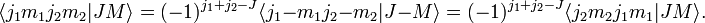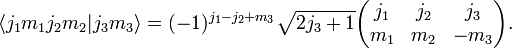Clebsch-Gordan coefficients
- This article presupposes knowledge of the quantum theory of angular momentum and angular momentum coupling.
In quantum mechanics, the Clebsch-Gordan coefficients (CG coefficients) are sets of numbers that arise in angular momentum coupling.
In mathematics, the CG coefficients appear in group representation theory, particularly of compact Lie groups. They arise in the explicit direct sum decomposition of the outer product of two irreducible representations (irreps) of a group G. In general the outer product representation (rep)—which is carried by a tensor product space—is reducible under G. Decomposition of the outer product rep into irreps of G requires a basis transformation of the tensor product space. The CG coefficients are the elements of the matrix of this basis transformation. In physics it is common to consider only orthonormal bases of the vector spaces involved, and then CG coefficients constitute a unitary matrix.
The name derives from the German mathematicians Alfred Clebsch (1833–1872) and Paul Gordan (1837–1912), who encountered an equivalent problem in invariant theory. An alternative name for the CG coefficients is Wigner coefficients, after Eugene Wigner (1902–1995).
The formulas below use Dirac's bra-ket notation, i.e., the quantity 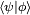 stands for a positive definite inner product between the elements ψ and φ of the same complex inner product space. We follow the physical convention
stands for a positive definite inner product between the elements ψ and φ of the same complex inner product space. We follow the physical convention
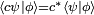 , where
, where 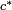 is the complex conjugate of the complex number c.
is the complex conjugate of the complex number c.
Contents |
[edit] Angular momentum CG coefficients
Although Clebsch-Gordan coefficients can be defined for arbitrary groups, we restrict our attention in this article to the groups associated with space and spin angular momentum, namely the groups SO(3) and SU(2). In that case CG coefficients can be defined as the expansion coefficients of total angular momentum eigenstates in an uncoupled tensor product basis. See the article angular momentum for the definition of angular momentum operators and their eigenstates. Since the definition of CG coefficients needs the definition of tensor products of angular momentum eigenstates, this will be given first.
From the formal definition recursion relations for the Clebsch-Gordan coefficients can be found. In order to settle the numerical values for the coefficients, a phase convention must be adopted. Below the Condon and Shortley phase convention is chosen.
[edit] Tensor product space
Let V1 be the 2j1 + 1 dimensional
vector space spanned by the eigenstates of 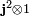 and
and 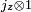
and V2 the 2j2 + 1 dimensional
vector space spanned by the eigenstates of 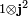 and
and 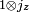
The tensor product of these spaces, 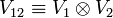 ,
has a (2j1 + 1)(2j2 + 1) dimensional uncoupled basis
,
has a (2j1 + 1)(2j2 + 1) dimensional uncoupled basis
Angular momentum operators acting on V12 can be defined by
and
Total angular momentum operators are defined by
The total angular momentum operators satisfy the commutation relations
showing that J is indeed an angular momentum operator. The quantity 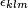 is the Levi-Civita symbol.
Hence total angular momentum eigenstates exist
is the Levi-Civita symbol.
Hence total angular momentum eigenstates exist
It can be derived—see, e.g., this article—that J must satisfy the triangular condition
The total number of total angular momentum eigenstates is equal to the dimension of V12
The total angular momentum states form an orthonormal basis of V12[1]
[edit] Formal definition of Clebsch-Gordan coefficients
The total angular momentum states can be expanded in the uncoupled basis
The expansion coefficients 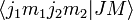 are called Clebsch-Gordan coefficients.
are called Clebsch-Gordan coefficients.
Applying the operator
to both sides of the defining equation shows that the Clebsch-Gordan coefficients can only be nonzero when
[edit] Recursion relations
Applying the total angular momentum raising and lowering operators, see e.g., this article,
to the left hand side of the defining equation gives
Applying the same operators to the right hand side gives
Combining these results gives recursion relations for the Clebsch-Gordan coefficients
Taking the upper sign with M = J gives
In the Condon and Shortley phase convention the coefficient
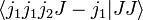 is taken
real and positive. With the last equation all other
Clebsch-Gordan coefficients
is taken
real and positive. With the last equation all other
Clebsch-Gordan coefficients 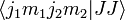 can be found. The normalization is fixed by the requirement that
the sum of the squares, which corresponds to the norm of the
state
can be found. The normalization is fixed by the requirement that
the sum of the squares, which corresponds to the norm of the
state 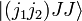 must be one.
must be one.
The lower sign in the recursion relation can be used to find all the Clebsch-Gordan coefficients with M = J − 1. Repeated use of that equation gives all coefficients.
This procedure to find the Clebsch-Gordan coefficients shows that they are all real (in the Condon and Shortley phase convention).
[edit] Explicit expression
The first derivation of an algebraic formula for CG coefficients was given by Wigner in his famous 1931 book. The following expression for the CG coefficients is due to Van der Waerden (1932) and is the most symmetric one of the various existing forms, see, e.g., Biedenharn and Louck (1981) for a derivation,
where
and the sum runs over all values of t which do not lead to negative factorials.
[edit] Orthogonality relations
These are most clearly written down by introducing the alternative notation
The first orthogonality relation is
and the second
[edit] Special cases
For 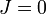 the Clebsch-Gordan coefficients are given by
the Clebsch-Gordan coefficients are given by
For 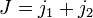 and
and 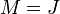 we have
we have
[edit] Symmetry properties
[edit] Relation to 3-jm symbols
Clebsch-Gordan coefficients are related to 3-jm symbols which have more convenient symmetry relations.
[edit] Notes
- ↑ The kets |(j1j2)JM⟩ and |JM⟩ denote the same state; the latter is used if it is not important that this state arose by coupling two states with angular momenta j1 and j2, or if the state arose in another way.


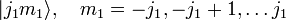
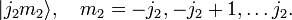
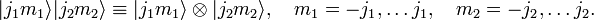
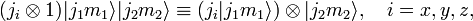
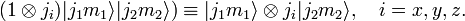
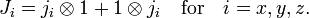
![[J_k,J_l] = i \sum_{m=x,y,z} \epsilon_{klm}J_m \,](../w/images/math/d/e/4/de47f892f12c64173c693d8f3359700e.png)
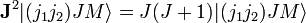
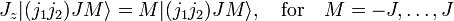
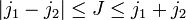
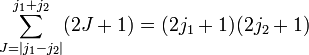
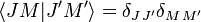
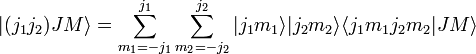
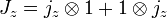
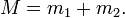
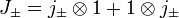
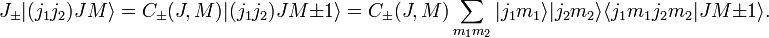
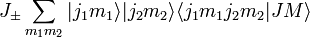
![=\sum_{m_1m_2}\left[ C_\pm(j_1,m_1)|j_1 m_1\pm 1\rangle |j_2m_2\rangle +C_\pm(j_2,m_2)|j_1 m_1\rangle |j_2 m_2\pm 1\rangle \right] \langle j_1 m_1 j_2 m_2|J M\rangle](../w/images/math/f/7/2/f72f39f117c39ff919f50038f032e9ad.png)
![= \sum_{m_1m_2} |j_1m_1\rangle|j_2m_2\rangle \left[ C_\pm(j_1,m_1\mp 1) \langle j_1 {m_1\mp 1} j_2 m_2|J M\rangle +C_\pm(j_2,m_2\mp 1) \langle j_1 m_1 j_2 {m_2\mp 1}|J M\rangle \right].](../w/images/math/8/2/9/82948bed290f30fb23cd3f95f09501d7.png)
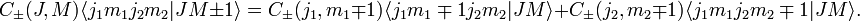

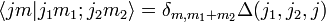
![\times \sum_t (-1)^t {\textstyle \frac{ \left[(2j+1) (j_1 +m_1 )! (j_1 -m_1)! (j_2 +m_2 )! (j_2 -m_2 )! (j+m)! (j-m)! \right]^{\frac{1}{2}}}{t! (j_1 +j_2 -j-t)! (j_1 -m_1 -t)! (j_2 +m_2 -t)! (j-j_2 +m_1 +t)! (j-j_1 -m_2 +t)!} }](../w/images/math/7/9/6/796ba37405d2c8667a5959d5af11a971.png)
![\Delta (j_1 ,j_2 ,j) \equiv \left[ \frac{ (j_1 +j_2 -j)! (j_1 -j_2 +j)! (-j_1 +j_2 +j)!} { (j_1 +j_2 +j+1)!}\right]^{{\frac{1}{2}}},](../w/images/math/1/9/0/1901a2a3f0d1af384b5a7c2bceef71ce.png)