Zipf distribution
In probability theory and statistics, the Zipf distribution and zeta distribution refer to a class of discrete probability distributions. They have been used to model the length distribution of words in a text, of text strings and keys in databases, and of the sizes of businesses and towns.
The Zipf distribution with parameter n assigns probability proportional to 1/r to an integer r ≤ n and zero otherwise, with normalization factor Hn, the n-th harmonic number.
A Zipf-like distribution with parameters n and s assigns probability proportional to 1/rs to an integer r ≤ n and zero otherwise, with normalization factor 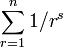 .
.
The zeta distribution with parameter s>1 assigns probability proportional to 1/rs to all integers r with normalization factor given by 1/ζ(s) where ζ(s) is the Riemann zeta function .
[edit] References
- Michael Woodroofe; Bruce Hill (1975). On Zipf's law, 425-434. Zbl 0343.60012.
| |
Some content on this page may previously have appeared on Citizendium. |

