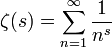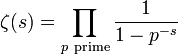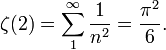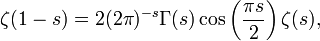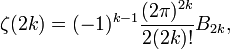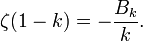Riemann zeta function
In mathematics, the Riemann zeta function, named after Bernhard Riemann, is one of the most important special functions. Its generalizations have important applications to number theory, arithmetic geometry, graph theory, and dynamical systems, to name a few examples. The Riemann zeta function in particular gained prominence when it was shown to have a connection with the distribution of the prime numbers. The most important aspect of the Riemann zeta function is the Riemann hypothesis, which was the 8th of Hilbert's Problems, and is one of the seven Millennium Prize Problems presented by the Clay Institute of Mathematics. As such, anyone who determines its truth or falsity is entitled to $1 million (U.S.)
Contents |
[edit] Definition
To understand this definition, you must already understand the concepts of complex exponents and infinite series of complex numbers.
The Riemann zeta function is a meromorphic function defined for complex numbers with real part 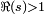 by the infinite series
by the infinite series
and then extended to all other complex values of s except s = 1 by analytic continuation. The function is holomorphic everywhere except for a simple pole at s = 1.
Euler's product formula for the zeta function is
(the variable p running through the set of prime numbers).
The celebrated Riemann hypothesis is the conjecture that all non-real values of s for which ζ(s) = 0 have real part 1/2. The problem of proving the Riemann hypothesis is the most well-known unsolved problem in mathematics.
[edit] History
The origin of the Riemann zeta function can be traced to the Basel problem. The solution to this problem states that
In deriving this identity, Leonard Euler also found the sums of the series ζ(2k) for 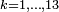 [1] These computations contain implicitly the germ of the idea of the zeta function.
According to Andre Weil, these and related results due to Euler remained as "mere curiosities, and virtually unknown, until they received new life at the hands of Riemann in 1859".[2]
[1] These computations contain implicitly the germ of the idea of the zeta function.
According to Andre Weil, these and related results due to Euler remained as "mere curiosities, and virtually unknown, until they received new life at the hands of Riemann in 1859".[2]
In an eight page paper, Riemann catapulted both himself and his namesake to worldwide renown. The paper includes the general definition of the zeta function (including the first use of the symbol ζ to denote it) and the proof of its analytic continuation, the functional equation (see below), as well as results relating the function to the distribution of prime numbers and of course, the Riemann hypothesis. Since then, the function and its relatives have found applications in myriad research papers in a vast array of fields.
Riemann is also responsible for naming the variable in the zeta function s, rather than the z which is more typically used for complex analytic functions. The now common (but strange) notation s = σ + it was introduced later.
[edit] The functional equation
The Riemann zeta function satisfies a functional equation:
where Γ(s) is the gamma function.
According to Andre Weil, Euler had already discovered the functional equation by the middle of the 18th century[3]. However, it remained virtually unknown until Riemann rediscovered it in his famous paper.
The equation can be interpreted as saying that the function has an imperfect symmetry around the critical line in the complex plane consisting of all complex numbers with real part equal to 1/2. For instance, the series definition of the zeta function and the functional equation in principle give one the means to compute values of the zeta function for all values outside of the critical strip, which consists of those complex numbers whose real part satisfies the inequalities 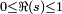 . (This assumes that one can compute the necessary values of the gamma function).
. (This assumes that one can compute the necessary values of the gamma function).
[edit] Zeroes
[edit] Special values
Aside from the special value 0, certain other values of the Riemann zeta function have been extensively studied. As mentioned above, Euler was the first to compute values of the zeta function when he found ζ(2k) for 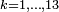 . In each case, he found that the value is a rational number times
. In each case, he found that the value is a rational number times 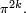 Later, he discovered a general formula, valid for all positive integers k:
Later, he discovered a general formula, valid for all positive integers k:
where B2k is a Bernoulli number. The functional equation allows us to convert this to a statement about the values of the zeta function at negative integers:
This is valid for every integer k > 0, as the values of the zeta function at nonpositive integers are all 0.
[edit] Generalizations
Analogues of the Riemann zeta function have been created in many different contexts. A unifying principle for these various zeta functions might be that they all are defined either through a series resembling the series defining the Riemann zeta function or through a product resembling the Eulerian product for the Riemann zeta function (or both!). More precisely, such a series definition typically extends over an index set of algebraic objects considered to be "integral" in some context, and the term corresponding to each object is a quotient whose denominator involves a rational integer defined in terms of the object raised to the -s power, where s is the function's variable. In contrast, the Euler product defining a zeta function typically extends over an index set of algebraic objects considered to be "prime" in some context, and the factor corresponding to each object again is a quotient whose denominator involves a rational integer defined in terms of the object raised to the -s power.
Other more general analogs of the Riemann zeta functions are called L-functions. A typical L-function is obtained from a zeta function by twisting the terms in the defining series or Eulerian product by including a factor of a character on the index set.
Important examples of zeta functions are:
- Artin-Mazur zeta function
- Dedekind zeta function
- Hasse-Weil zeta function
- Igusa zeta function
- Ihara zeta function
- partial zeta function
- p-adic zeta function
- Selberg zeta function
Here is a directory of known zeta functions.
Important examples of L-functions are:
- Artin L-function
- Dirichlet L-function
- Hasse-Weil L-function
- Hecke L-function
- modular L-function
- Motivic L-function
- p-adic L-function
- ↑ See William Dunham, Journey Through Genius.
- ↑ Andre Weil, Basic Number Theory, p.185.
- ↑ Andre Weil, Basic Number Theory, p.185
| |
Some content on this page may previously have appeared on Citizendium. |