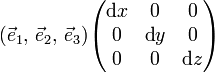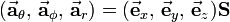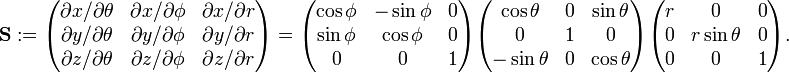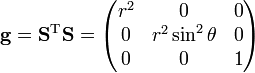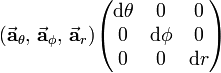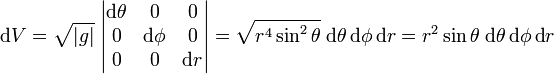Triple product
In linear algebra, a triple product is a common term for a product of three vectors A, B, and C leading to a scalar (a number). The absolute value of this scalar is the volume V of the parallelepiped spanned by the three vectors:
where B × C is the cross product of two vectors (resulting into a vector) and the dot indicates the inner product between two vectors (a scalar).
The triple product is sometimes called the scalar triple product to distinguish it from the vector triple product A×(B×C). The scalar triple product is often written as [A B C]. The vector triple product can be expanded by the aid of the baccab formula.
Contents |
[edit] Explanation
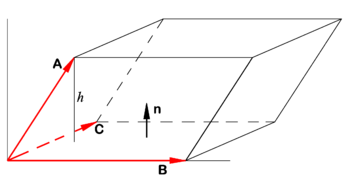
Let n be a unit normal to the parallelogram spanned by B and C (see figure). Let h be the height of the terminal point of the vector A above the base of the parallelepiped. Recall:
- Volume V of parallelepiped is height h times area S of the base.
Note that h is the projection of A on n and that the area S is the length of the cross product of the vectors spanning the base,
Use
where it is used that
(The unit normal n has the direction of the cross product B × C).
If A, B, and C do not form a right-handed system, A•n < 0 and we must take the absolute value: | A• (B×C)|.
[edit] Triple product as determinant
Take three orthogonal unit vectors i , j, and k and write
The triple product is equal to a 3 × 3 determinant
Indeed, writing the cross product as a determinant we find
Since a determinant is invariant under cyclic permutation of its columns, it follows
[edit] Arbitrary basis
The fact that the triple product represents the volume of a geometric figure (a parallelepiped) suggests that it must be possible to express the volume with respect to any (even a non-orthonormal) basis.
In the derivation of a general equation for the volume, a minor change of notation is needed, since it is essential to distinguish a component vector (bold) from a geometric vector (arrow on top). The following substitutions are made:
An arbitrary (possibly non-orthonormal) basis 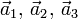 of Euclidean 3-space is connected by a 3×3 non-singular matrix S to an orthonormal basis basis,
of Euclidean 3-space is connected by a 3×3 non-singular matrix S to an orthonormal basis basis,
The representation g′ of the metric tensor with respect to the new basis becomes
(It is exactly this equation that shows that the gij are the components of a tensor). Although the unprimed metric tensor g is represented by an identity matrix, it will be carried along. In matrix language
where the following two rules for determinants (numbers) were used
and the determinants of g and g′, are written as g and g′, respectively. From:
follows
Note that the component vectors A = (A1, A2, A3) and A′ = (A1′, A2′, A3′) represent the same geometric vector 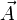 . The same transformation rule holds for the components of the geometric vectors
. The same transformation rule holds for the components of the geometric vectors  and
and  . By design the three primed component vectors span the same parallelepiped as the original unprimed component vectors.
In terms of matrices the transformation rule is,
. By design the three primed component vectors span the same parallelepiped as the original unprimed component vectors.
In terms of matrices the transformation rule is,
where the general rule
is used.
This result shows that the generalized expression for the volume V (a real positive number, which is why absolute values are taken) of the parallelepiped
is invariant under any basis transformation and represents always the volume of the same parallelepiped, irrespective of the choice of basis.
If A, B, and C are the component vectors of  with respect to an orthonormal basis then g = I. The identity matrix has unit determinant, so that the earlier expression for the volume is indeed recovered as a special case.
with respect to an orthonormal basis then g = I. The identity matrix has unit determinant, so that the earlier expression for the volume is indeed recovered as a special case.
[edit] Examples
The infinitesimal volume element dV spanned by the following three orthogonal vectors
is equal to dV = dxdydx because g = I and the determinant of a diagonal matrix is equal to the product of the diagonal elements.
Similarly for spherical polar coordinates
with
The metric tensor is
The volume element spanned by the following three orthogonal (non-unit) vectors
is equal to (vertical bars around the array indicate a determinant):
Note that r²sinθ ≥ 0 for 0 ≤ θ ≤ π.
[edit] Reference
M. R. Spiegel, Theory and Problems of Vector Analysis, Schaum Publishing, New York (1959) p. 26


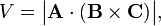
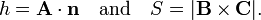
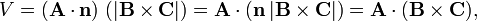
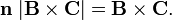
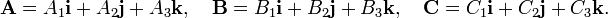
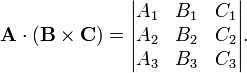
![\begin{align}
\mathbf{A}\cdot(\mathbf{B}\times\mathbf{C}) &=
\mathbf{A}\cdot \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
B_1 & B_2 & B_3 \\
C_1 & C_2 & C_3 \\
\end{vmatrix} \\
&= \big(A_1\mathbf{i}+ A_2\mathbf{j}+A_3\mathbf{k}\big)\cdot
\big[ (B_2\,C_3 - B_3\,C_2)\;\mathbf{i}+ (B_3\,C_1 - B_1\,C_3)\;\mathbf{j} +
(B_1\,C_2 - B_2\,C_1)\;\mathbf{k} \big] \\
&= A_1\;(B_2\,C_3 - B_3\,C_2)+ A_2\;(B_3\,C_1 - B_1\,C_3) + A_3\;(B_1\,C_2 - B_2\,C_1)\\
&=\begin{vmatrix}
A_1 & B_1 & C_1 \\
A_2 & B_2 & C_2 \\
A_3 & B_3 & C_3 \\
\end{vmatrix} .
\end{align}](../w/images/math/1/6/d/16d14aac2e4ddcaff7c893e178e4badb.png)
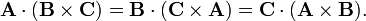
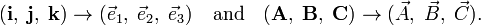

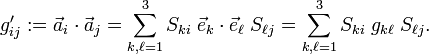
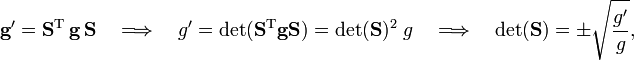
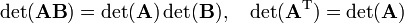
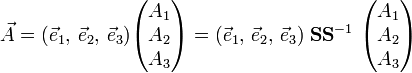
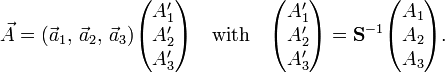
![\begin{pmatrix}
A_1' & B_1' & C_1' \\
A_2' & B_2' & C_2' \\
A_3' & B_3' & C_3' \\
\end{pmatrix} =
\mathbf{S}^{-1}
\begin{pmatrix}
A_1 & B_1 & C_1 \\
A_2 & B_2 & C_2 \\
A_3 & B_3 & C_3 \\
\end{pmatrix} \quad \Longrightarrow\quad
\det[\mathbf{A}'\; \mathbf{B}' \; \mathbf{C}'] = \pm\sqrt{\frac{g}{g'}}\;
\det[\mathbf{A}\; \mathbf{B} \; \mathbf{C}]](../w/images/math/f/a/d/fadbf4a8568d5943c0cdc364bc527d0f.png)
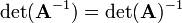
![V = \sqrt{|g|}\;\; \big\vert\det[\mathbf{A} \; \mathbf{B}\; \mathbf{C}]\,\big\vert](../w/images/math/a/2/e/a2e8eef6176f9943935a979ccb5c3340.png)