Compactness axioms
From Knowino
(Redirected from Sequentially compact)
In general topology, the important property of compactness has a number of related properties.
The definitions require some preliminary terminology. A cover of a set X is a family 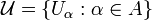 such that the union
such that the union 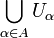 is equal to X. A subcover is a subfamily which is again a cover
is equal to X. A subcover is a subfamily which is again a cover 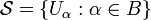 where B is a subset of A. A refinement is a cover
where B is a subset of A. A refinement is a cover 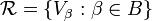 such that for each β in B there is an α in A such that
such that for each β in B there is an α in A such that 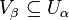 . A cover is finite or countable if the index set is finite or countable. A cover is point finite if each element of X belongs to a finite numbers of sets in the cover. The phrase "open cover" is often used to denote "cover by open sets".
. A cover is finite or countable if the index set is finite or countable. A cover is point finite if each element of X belongs to a finite numbers of sets in the cover. The phrase "open cover" is often used to denote "cover by open sets".
[edit] Definitions
We say that a topological space X is
- Compact if every cover by open sets has a finite subcover.
- A compactum if it is a compact metric space.
- Countably compact if every countable cover by open sets has a finite subcover.
- Lindelöf if every cover by open sets has a countable subcover.
- Sequentially compact if every convergent sequence has a convergent subsequence.
- Paracompact if every cover by open sets has an open locally finite refinement.
- Metacompact if every cover by open sets has a point finite open refinement.
- Orthocompact if every cover by open sets has an interior preserving open refinement.
- σ-compact if it is the union of countably many compact subspaces.
- Locally compact if every point has a compact neighbourhood.
- Strongly locally compact if every point has a neighbourhood with compact closure.
- σ-locally compact if it is both σ-compact and locally compact.
- Pseudocompact if every continuous real-valued function is bounded.
| |
Some content on this page may previously have appeared on Citizendium. |
