Scheme (mathematics)
Schemes, and functions between them, are the principal objects of study in modern algebraic geometry. Algebraic geometry began as the study of varieties, geometric figures described by polynomial equations with coefficents in a field. The geometric properties of an affine variety are reflected in algebraic properties in its ring of functions, which is the quotient of a polynomial ring. These algebraic properties can be defined in the context of arbitrary commutative rings, and affine schemes are the corresponding geometric objects. A general scheme is a geometric object which looks like an affine scheme in a neighborhood of every point.
Schemes have superseded varieties as the main objects of interest in algebraic geometry for several reasons: they give a uniform way to treat all previous disparate definitions of varieties, including affine, projective, quasi-projective, and abstract varieties, and there is a huge diversity of schemes that are not classical varieties. Also, the theory of varieties is most successful when the points on the varieties have values in an algebraically closed field. By contrast, important problems in arithmetic geometry involve studying arithmetic properties of points on varieties, which cannot be done by working over an algebraically closed field. Schemes have proven to be effective at overcoming this difficulty.
The theory of schemes was pioneered by Alexander Grothendieck. The foundations of scheme theory were initially organized in Grothendieck's multi-volume work Éléments de Géométrie Algébrique with the assistance of Jean Dieudonné.
A number of technical definitions and procedures are outlined in the glossary of scheme theory.
[edit] The Category of Schemes
A scheme 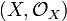 consists of a topological space X together with a sheaf
consists of a topological space X together with a sheaf 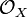 of rings (called the structural sheaf on X) such that every point of X has an open neighborhood U such that the locally ringed space
of rings (called the structural sheaf on X) such that every point of X has an open neighborhood U such that the locally ringed space 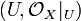 is isomorphic to an affine scheme.
is isomorphic to an affine scheme.
Projective schemes constitute an important class of schemes, especially for the study of curves.
The category of schemes is defined by taking morphisms of schemes to be morphisms of locally ringed spaces. Many kinds of morphisms of schemes are characterized affine-locally, in the sense that
[edit] Gluing Properties
The notion of "gluing" is one of the central ideas in the theory of schemes. Let S be a scheme, and
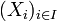 a family of S-schemes. If we're given families
a family of S-schemes. If we're given families 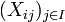 and S-isomorphisms
and S-isomorphisms 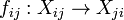 such that:
such that: 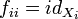 ,
, 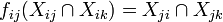 , and
, and 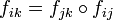 on
on 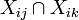 for all
for all 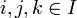 , then there is an S-scheme X together with S-immersions
, then there is an S-scheme X together with S-immersions 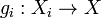 such that
such that 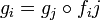 on Xij and so that
on Xij and so that 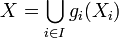 . This scheme X is called the gluing over S of the Xi along the Xij.
. This scheme X is called the gluing over S of the Xi along the Xij.
The S-scheme X is universal for the property above: i.e., for any S-scheme Z and family of morphisms 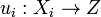 such that
such that 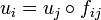 on Xij, there is a unique morphism
on Xij, there is a unique morphism 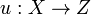 such that
such that 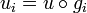 . Moreover, if Z is a scheme, then giving a morphism
. Moreover, if Z is a scheme, then giving a morphism 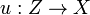 is equivalent to giving an
open covering
is equivalent to giving an
open covering 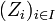 of Z and morphisms
of Z and morphisms 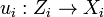 such that
such that 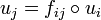 on
on 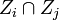 .
.
[edit] Morphisms of Schemes
| |
Some content on this page may previously have appeared on Citizendium. |

