Polynomial ring
In algebra, the polynomial ring over a ring is a construction of a ring which formalises the polynomials of elementary algebra.
Contents |
[edit] Construction of the polynomial ring
Let R be a ring. Consider the R-module of sequences
which have only finitely many non-zero terms, under pointwise addition
We define the degree of a non-zero sequence (an) as the the largest integer d such that ad is non-zero.
We define "convolution" of sequences by
Convolution is a commutative, associative operation on sequences which is distributive over addition.
Let X denote the sequence
We have
and so on, so that
which makes sense as a finite sum since only finitely many of the an are non-zero.
The ring defined in this way is denoted R[X].
[edit] Alternative points of view
We can view the construction by sequences from various points of view
We may consider the set of sequences described above as the set of R-valued functions on the set N of natural numbers (including zero) and defining the support of a function to be the set of arguments where it is non-zero. We then restrict to functions of finite support under pointwise addition and convolution.
We may further consider N to be the free monoid on one generator. The functions of finite support on a monoid M form the monoid ring R[M].
[edit] Properties
- The polynomial ring R[X] is an algebra over R.
- If R is commutative then so is R[X].
- If R is an integral domain then so is R[X].
- In this case the degree function satisfies deg(fg) = deg(f) + deg(g).
- If R is a unique factorisation domain then so is R[X].
- Hilbert's basis theorem: If R is a Noetherian ring then so is R[X].
- If R is a field, then R[X] is a Euclidean domain.
- If
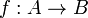 is a ring homomorphism then there is a homomorphism, also denoted by f, from
is a ring homomorphism then there is a homomorphism, also denoted by f, from ![A[X] \rarr B[X]](../w/images/math/6/e/6/6e6d41f379158136c4445a65b5b135aa.png) which extends f. Any homomorphism on A[X] is determined by its restriction to A and its value at X.
which extends f. Any homomorphism on A[X] is determined by its restriction to A and its value at X.
[edit] Multiple variables
The polynomial ring construction may be iterated to define
but a more general construction which allows the construction of polynomials in any set of variables 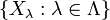 is to follow the initial construction by taking S to be the Cartesian power
is to follow the initial construction by taking S to be the Cartesian power 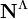 and then to consider the R-valued functions on S with finite support.
and then to consider the R-valued functions on S with finite support.
We see that there are natural isomorphisms
We may also view this construction as taking the free monoid S on the set Λ and then forming the monoid ring R[S].
[edit] References
- Serge Lang (1993). Algebra, 3rd ed. Addison-Wesley, 97-98. ISBN 0-201-55540-9.
| |
Some content on this page may previously have appeared on Citizendium. |

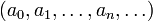
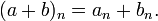
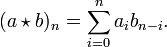
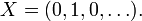
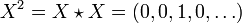
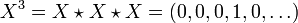
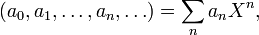
![R[X_1,X_2,\ldots,X_n] = R[X_1][X_2]\ldots[X_n] ,\,:](../w/images/math/0/8/3/083773a31579e2f4379cdc3137309d95.png)
![R[X_1][X_2] \equiv R[X_1,X_2] \equiv R[X_2][X_1] .\,](../w/images/math/5/6/9/5697928c9be73b87a06c76089bb79f14.png)