Quantum operation

From Knowino
Jump to: navigation, search

In physics, in particular in mathematical physics, a quantum operation is a mathematical formalism used to describe general transformations of states of a quantum (mechanical) system. The state of a quantum system on a Hilbert space 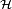\scriptstyle \mathcal{H} is represented by a non-negative definite trace class operator on 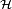\scriptstyle \mathcal{H} with trace equal to one. Such operators are called density operators. However, the quantum operation formalism is not defined on density operators, but rather on a more general class of non-negative definite trace class operators that need not have trace one, that is the class that is sometimes referred to as unnormalized density operators.

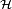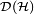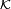Suppose that the class of unnormalized density operators on a Hilbert space \scriptstyle \mathcal{H} is denoted by \scriptstyle \mathcal{D}(\mathcal{H}). Let \scriptstyle \mathcal{K} be another Hilbert space (can be the same as 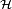\scriptstyle \mathcal{H}). 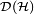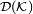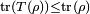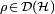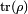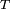A quantum operation T is a linear map that takes any element of \scriptstyle \mathcal{D}(\mathcal{H}) and sends it to an element of \scriptstyle \mathcal{D}(\mathcal{K}) with the property that \scriptstyle {\rm tr}(T(\rho)) \leq {\rm tr}(\rho) for all \scriptstyle \rho \,\in\, \mathcal{D}(\mathcal{H}), where \scriptstyle {\rm tr}(\rho) denotes the trace of \scriptstyle \rho, and \scriptstyle T is a completely positive map.

To illustrate, consider the projective measurement of an observable (i.e., a self-adjoint, densely defined operator) X of a quantum system 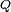\scriptstyle Q with Hilbert space 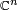\scriptstyle \mathbb{C}^n, and suppose that X has eigenvalues λk and a corresponding set of orthonormal eigenvectors 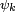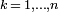\scriptstyle \psi_k, \scriptstyle k\,=\,1,\ldots,n. 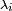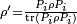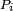Say that the density operator of the system prior to measurement is \scriptstyle \rho , then after a projective measurement of X is performed and the outcome observed is \scriptstyle \lambda_i the state transforms \scriptstyle \rho to a new state \scriptstyle \rho'=\frac{P_i \rho P_i}{{\rm tr}(P_i \rho P_i)}, where \scriptstyle P_i is the projection operator 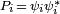\scriptstyle P_i\,=\,\psi_i \psi_i^*. 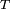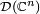The quantum operation associated with this measurement is a linear map \scriptstyle T from \scriptstyle \mathcal{D}(\mathbb{C}^n) to itself acting as 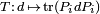\scriptstyle T:\, d \,\mapsto\, {\rm tr}(P_i d P_i) . Therefore, the density operator 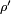\scriptstyle \rho' after the measurement can just be written as a normalized version of 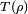\scriptstyle T(\rho) (that is, normalized to have trace one).

To look at a slightly more complicated example than the one in the previous paragraph, imagine that we now have an infinite ensemble of identical copies of the quantum system 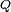\scriptstyle Q and a projective measurement of X is performed on each copy of 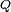\scriptstyle Q. 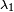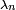Furthermore, suppose that we perform a selective measurement on this ensemble by discarding, after the measurements have been made, all systems in the ensemble whose measurement outcome is not \scriptstyle \lambda_1 or \scriptstyle \lambda_n . Now, if each system in the ensemble was identically prepared in a state with density operator ρ then the density operator of the reduced ensemble after selective measurement can be described via the quantum operation 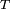\scriptstyle T given by 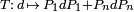\scriptstyle T:\, d \,\mapsto \, P_1 d P_1 + P_n d P_n. 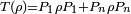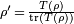That is, \scriptstyle T(\rho)= P_1 \rho P_1 + P_n \rho P_n and the density operator ρ' of the post-measurement ensemble is simply \scriptstyle \rho' \,=\, \frac{T(\rho)}{{\rm tr}(T(\rho))}.

Descriptions of more complex transformation of the state of an ensemble of quantum systems can be conveniently given using the language of quantum operation valued measures.

Information.svg Some content on this page may previously have appeared on Citizendium.
Retrieved from "http://knowino.org/wiki/Quantum_operation"
Personal tools
Variants
Actions
Navigation
Community
Toolbox