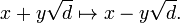Quadratic field
In mathematics, a quadratic field is a field which is an extension of its prime field of degree two.
In the case when the prime field is finite, so is the quadratic field, and we refer to the article on finite fields. In this article we treat quadratic extensions of the field Q of rational numbers.
In characteristic zero, every quadratic equation is soluble by taking one square root, so a quadratic field is of the form 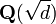 for a non-zero non-square rational number d. Multiplying by a square integer, we may assume that d is in fact a square-free integer.
for a non-zero non-square rational number d. Multiplying by a square integer, we may assume that d is in fact a square-free integer.
Contents |
[edit] Ring of integers
As above, we take d to be a square-free integer. The maximal order of F is
unless 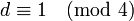 in which case
in which case
[edit] Discriminant
The field discriminant of F is d if 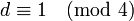 and otherwise 4d.
and otherwise 4d.
[edit] Unit group
If d is negative, then the only units in the ring of integers are roots of unity. If d is positive, the unit group has rank one, with a fundamental unit of infinite order.
[edit] Class group
[edit] Splitting of primes
The prime 2 is ramified if  . If
. If 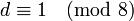 then 2 splits into two distinct prime ideals, and if
then 2 splits into two distinct prime ideals, and if 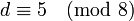 then 2 is inert.
then 2 is inert.
An odd prime p ramifies iff p divides d. Otherwise, p splits or is inert according as the Legendre symbol  is +1 or -1 respectively.
is +1 or -1 respectively.
[edit] Galois group
The extension F/Q is generated by the roots of X2 − d and both roots lie in the field, which is thus a splitting field and so a Galois extension. The Galois group is cyclic of order two, with the non-trivial element being the field automorphism
If F is a complex quadratic field then this automorphism is induced by complex conjugation.
[edit] References
- A. Fröhlich; M.J. Taylor (1991). Algebraic number theory. Cambridge University Press, 175-193,220-230,306-309. ISBN 0-521-36664-X.
- I.N. Stewart; D.O. Tall (1979). Algebraic number theory. Chapman and Hall, 59-62. ISBN 0-412-13840-9.
- Pierre Samuel (1972). Algebraic number theory. Hermann/Kershaw, 34-36.
| |
Some content on this page may previously have appeared on Citizendium. |


![O_F = \mathbf{Z}[\sqrt d] \,](../w/images/math/1/9/f/19f366ce263efac249a95d65ff06275e.png)
![O_F = \mathbf{Z}\left[\frac{1+\sqrt d}{2}\right] .](../w/images/math/8/d/0/8d08353ac9a3672adc411ab5c61b8149.png)