Finite field
A finite field is a field with a finite number of elements; e,g, the fields 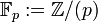 (with the addition and multiplication induced from the
same operations on the integers). For any prime number p, and natural number n, there exists a unique finite field with pn elements; this
field is denoted by
(with the addition and multiplication induced from the
same operations on the integers). For any prime number p, and natural number n, there exists a unique finite field with pn elements; this
field is denoted by 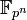 or
or 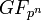 (where GF stands for "Galois field").
(where GF stands for "Galois field").
Contents |
[edit] Proofs of basic properties:
[edit] Finite characteristic:
Let F be a finite field, then by the pigeonhole principle there are two different natural numbers number n, m such that 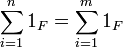 .
Hence there is some minimal natural number N such that
.
Hence there is some minimal natural number N such that 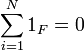 . Since F is a field, it has no divisors of 0, and hence N is prime.
. Since F is a field, it has no divisors of 0, and hence N is prime.
[edit] Existence and uniqueness of Fp
To begin with it is follows by inspection that 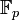 is a field. Furthermore, given any other field F with p elements, one immediately get an isomorphism
is a field. Furthermore, given any other field F with p elements, one immediately get an isomorphism 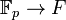 by mapping
by mapping 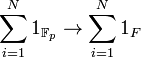 for all N.
for all N.
[edit] Existence - general case
Working over 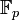 , let
, let 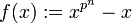 . Let F be the splitting field of f over
. Let F be the splitting field of f over 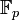 .
Note that f' = − 1, and hence the gcd of f, f' is 1, and all the roots of f in F are distinct. Furthermore, note that the set of roots of f is closed under addition and multiplication; hence
F is simply the set of roots of f.
.
Note that f' = − 1, and hence the gcd of f, f' is 1, and all the roots of f in F are distinct. Furthermore, note that the set of roots of f is closed under addition and multiplication; hence
F is simply the set of roots of f.
[edit] Uniqueness - general case
Let F be a finite field of characteristic p, then it contains 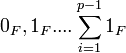 ; i.e. it contains a copy of
; i.e. it contains a copy of 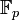 .
Hence, F is a vector field of finite dimension over
.
Hence, F is a vector field of finite dimension over 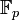 . Moreover since the non-zero elements of F form a group, they are all roots of the polynomial
. Moreover since the non-zero elements of F form a group, they are all roots of the polynomial
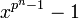 ; hence the elements of F are all roots of this polynomial.
; hence the elements of F are all roots of this polynomial.
[edit] The Frobenius map
Let F be a field of characteristic p, then the map 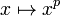 is the generator of the Galois group
is the generator of the Galois group 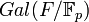 .
.
| |
Some content on this page may previously have appeared on Citizendium. |

