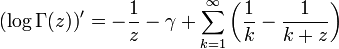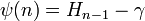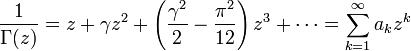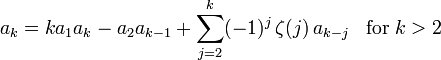Polygamma function
In mathematics, the polygamma functions are the logarithmic derivatives of the gamma function. The polygamma function of order m is defined as
The case 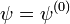 is called the digamma function.
is called the digamma function.
Taking the logarithm of Weierstrass's product for the gamma function, we can write the logarithm of the gamma function in the form of a series
Differentiating termwise renders the logarithmic derivative of the gamma function
which is called the digamma function, denoted by 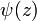 . The expression for the digamma function is simpler than the series we started with, all logarithms notably absent. If z = n, a positive integer, all but finitely many terms in the series cancel and we are left with
. The expression for the digamma function is simpler than the series we started with, all logarithms notably absent. If z = n, a positive integer, all but finitely many terms in the series cancel and we are left with
where Hn is the harmonic number 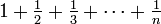 . As it generalizes harmonic numbers to non-integer indices, we could say that the digamma function is to harmonic numbers as the gamma function is to the factorials. Since (logf)' = f' / f, we can recover the ordinary derivative of the gamma function as Γ'(z) = Γ(z)ψ(z); the derivative at an integer is then Γ'(n) = (Hn − 1 − γ)(n − 1)! and in particular, Γ'(1) = − γ, providing a geometric interpretation of Euler's constant as the slope of the gamma function's graph at 1.
. As it generalizes harmonic numbers to non-integer indices, we could say that the digamma function is to harmonic numbers as the gamma function is to the factorials. Since (logf)' = f' / f, we can recover the ordinary derivative of the gamma function as Γ'(z) = Γ(z)ψ(z); the derivative at an integer is then Γ'(n) = (Hn − 1 − γ)(n − 1)! and in particular, Γ'(1) = − γ, providing a geometric interpretation of Euler's constant as the slope of the gamma function's graph at 1.
Continuing in a similar manner, rational series for the polygamma functions of higher order can be derived.
The polygamma functions are related to the Riemann zeta function: it can be shown that the polygamma function at an integer value is expressible in terms of the zeta function at integers. With the higher-order derivatives available, it becomes possible to calculate the Taylor series of the gamma function around any integer in terms of Euler's constant and the zeta function. Choosing 1 / Γ(z) instead of Γ(z) for convenience, since the former is an entire function and hence has an everywhere convergent Taylor series in the simple point z = 0, we can compute
where a1 = 1, a2 = γ,
and 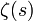 is the Riemann zeta function.
is the Riemann zeta function.
| |
Some content on this page may previously have appeared on Citizendium. |

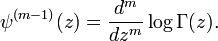
![\log \Gamma(z) = -\log z -\gamma z + \sum_{k=1}^\infty \left[ \frac{z}{k} - \log\left(1+\frac{z}{k}\right) \right].](../w/images/math/a/6/8/a68f1812d7a3e302a95ff942ae39bbf1.png)