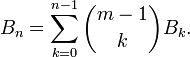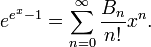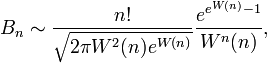Partition (mathematics)
In mathematics, partition refers to two related concepts, in set theory and number theory.
Contents |
[edit] Partition (set theory)
A partition of a set X is a collection  of non-empty subsets ("parts") of X such that every element of X is in exactly one of the subsets in
of non-empty subsets ("parts") of X such that every element of X is in exactly one of the subsets in 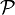 .
.
Hence a three-element set {a,b,c} has 5 partitions:
- {a,b,c}
- {a,b}, {c}
- {a,c}, {b}
- {b,c}, {a}
- {a}, {b}, {c}
Partitions and equivalence relations give the same data: the equivalence classes of an equivalence relation on a set X form a partition of the set X, and a partition 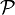 gives rise to an equivalence relation where two elements are equivalent if they are in the same part from
gives rise to an equivalence relation where two elements are equivalent if they are in the same part from 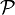 .
.
The number of partitions of a finite set of size n into k parts is given by a Stirling number of the second kind;
[edit] Bell numbers
The total number of partitions of a set of size n is given by the n-th Bell number, denoted Bn. These may be obtained by the recurrence relation
They have an exponential generating function
Asymptotically,
where W denotes the Lambert W function.
[edit] Partition (number theory)
A partition of an integer n is an expression of n as a sum of positive integers ("parts"), with the order of the terms in the sum being disregarded.
Hence the number 3 has 3 partitions:
- 3
- 2+1
- 1+1+1
The number of partitions of n is given by the partition function p(n).
[edit] References
- Chen Chuan-Chong; Koh Khee-Meng (1992). Principles and Techniques of Combinatorics. World Scientific. ISBN 981-02-1139-2.
| |
Some content on this page may previously have appeared on Citizendium. |