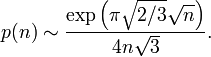Partition function (number theory)
From Knowino
In number theory the partition function p(n) counts the number of partitions of a positive integer n, that is, the number of ways of expressing n as a sum of positive integers (where order is not significant).
Thus p(3) = 3, since the number 3 has 3 partitions:
- 3
- 2+1
- 1+1+1
[edit] Properties
The partition function satisfies an asymptotic relation
| |
Some content on this page may previously have appeared on Citizendium. |