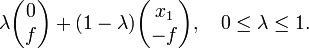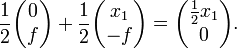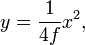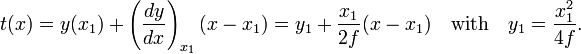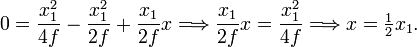Parabola
A parabola is the planar curve formed by the points that lie as far from a given line (the directrix) as from a given point (the focus). Alternatively, a parabola is the curve you get when intersecting a right circular cone with a plane parallel to a generator of the cone (a line on the cone which goes through its apex); thus, a parabola is a conic section.
If the focus lies on the directrix, then the "parabola" is in fact a line. In the language of conic sections, this corresponds to the case when the plane contains a generator of the cone.
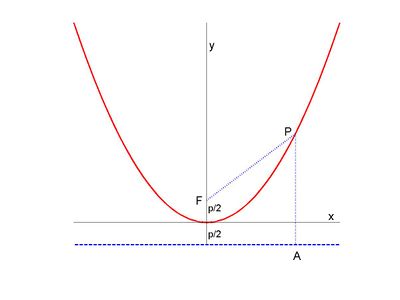
To avoid this degenerate case, we assume that the focus lies not on the directrix. The line through the focus and perpendicular to the directrix is called the axis of the parabola. It is the unique line of symmetry of the parabola. The parabola has one point that lies on the axis. This point is called the vertex of the parabola. The distance between the focus and the vertex is called the focal distance of the parabola. It is the same as the distance between the vertex and the directrix, and half the distance from the focus to the directrix.
The shape of a parabola is determined by the focal distance. All parabolas with the same focal distance are congruent, meaning that given any parabola can be moved to any other parabola with the same focal distance by a rigid motion.
[edit] Parabolic mirror
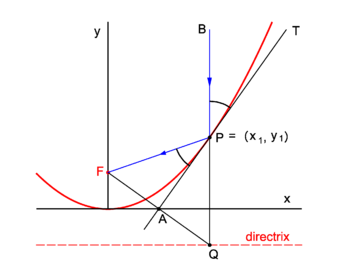
Parabolic mirrors concentrate incoming vertical light beams in their focus. We show this.
Consider in figure 2 the arbitrary vertical light beam B (blue, parallel to the y-axis) that enters the parabola and hits it at point P = (x1, y1). The parabola (red) has focus in point F. The incoming beam is reflected at P obeying the well-known law: incidence angle is equal to angle of reflection. The angles involved are with the line APT which is tangent to the parabola at point P. It will be shown that the reflected beam passes through F.
Clearly ∠BPT = ∠APQ (they are vertically opposite angles). Further ∠APQ = ∠FPA because the triangles FPA and QPA are congruent and hence ∠FPA (angle of reflection) is equal to ∠BPT (angle of incidence).
We prove the congruence of the triangles: By the definition of the parabola the line segments FP and QP are of equal length, because the length of the latter segment is the distance of P to the directrix and the length of FP is the distance of P to the focus. The point F has the coordinates (0,f) and the point Q has the coordinates (x1, −f). The line segment FQ has the equation
The midpoint A of FQ has coordinates (λ = ½):
Hence A lies on the x-axis. The parabola has equation,
and the equation of the tangent at P is
This line intersects the x-axis at t = 0,
The intersection of the tangent with the x-axis is the point A = (½x1, 0) that—as was just shown—lies on the midpoint of FQ. The corresponding sides of the triangles FPA and QPA are of equal length and hence the triangles are congruent.
Finally, it is of interest (but unimportant for the proof) to remark that AP is orthogonal to FQ and hence that points F and Q are related by orthogonal reflection in the tangent line AT.
| |
Some content on this page may previously have appeared on Citizendium. |