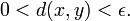Limit point
In topology, a limit point (or "accumulation point") of a subset S of a topological space X is a point x that cannot be separated from S.
Contents |
[edit] Definition
Formally, x is a limit point of S if every neighbourhood of x contains a point of S other than x itself.
A limit point of S need not belong to S, but may belong to it.
[edit] Metric space
In a metric space (X,d), a limit point of a set S may be defined as a point x such that for all ε > 0 there exists a point y in S such that
This agrees with the topological definition given above.
[edit] Properties
- A subset S is closed if and only if it contains all its limit points.
- The closure of a set S is the union of S with its limit points.
[edit] Derived set
The derived set of S is the set of all limit points of S. A point of S which is not a limit point is an isolated point of S. A set with no isolated points is dense-in-itself. A set is perfect if it is closed and dense-in-itself; equivalently a perfect set is equal to its derived set.
[edit] Related concepts
[edit] Limit point of a sequence
A limit point of a sequence (an) in a topological space X is a point x such that every neighbourhood U of x contains all points of the sequence with numbers above some n(U). A limit point of the sequence (an) need not be a limit point of the set {an}.
[edit] Adherent point
A point x is an adherent point or contact point of a set S if every neighbourhood of x contains a point of S (not necessarily distinct from x).
[edit] ω-Accumulation point
A point x is an ω-accumulation point of a set S if every neighbourhood of x contains infinitely many points of S.
[edit] Condensation point
A point x is a condensation point of a set S if every neighbourhood of x contains uncountably many points of S.
[edit] References
- Wolfgang Franz (1967). General Topology. Harrap, 23.
- Lynn Arthur Steen; J. Arthur Seebach jr (1978). Counterexamples in Topology. Berlin, New York: Springer-Verlag, 5-6. ISBN 0-387-90312-7.
| |
Some content on this page may previously have appeared on Citizendium. |