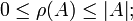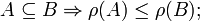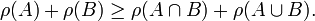Matroid

In mathematics, a matroid or independence space is a structure that generalises the concept of linear and algebraic independence.

An independence structure on a ground set E is a family 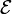of subsets of E, called independent sets, with the properties

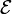• is a downset, that is, ;
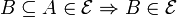• The exchange property: if 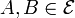with | B | = | A | + 1 then there exists 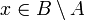such that .

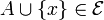A basis in an independence structure is a maximal independent set. Any two bases have the same number of elements. A circuit is a minimal dependent set. Independence spaces can be defined in terms of their systems of bases or of their circuits.

[edit] Examples

The following sets form independence structures:

• ;
• ;
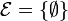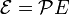• Linearly independent sets in a vector space;
• Algebraically independent sets in a field extension;
• Affinely independent sets in an affine space;
• Forests in a graph.

[edit] Rank

We define the rank ρ(A) of a subset A of E to be the maximum cardinality of an independent subset of A. The rank satisfies the following

The last of these is the submodular inequality.

A flat is a subset A of E such that the rank of A is strictly less than the rank of any proper superset of A.

[edit] References

• Victor Bryant; Hazel Perfect (1980). Independence Theory in Combinatorics. Chapman and Hall. ISBN 0-412-22430-5. 
• James Oxley (1992). Matroid theory. Oxford University Press. ISBN 0-19-853563-5. 

Some content on this page may previously have appeared on Citizendium.