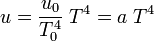Ludwig Boltzmann
Ludwig Eduard Boltzmann (Vienna, 20 February 1844 – Duino near Trieste, 5 September 1906) was an Austrian theoretical physicist best known for his contributions to atomic theory and statistical thermodynamics.[1]
His name lives on in the constant of Boltzmann kB (one of the most ubiquitous natural constants), in the Boltzmann factor exp[-E/(kBT)] (the probability that a physical system with absolute temperature T is in a thermodynamical state with energy E), Boltzmann's H theorem (entropy increases as a function of time in irreversible processes), the Boltzmann equation (describes how a velocity distribution of an ideal gas evolves toward equilibrium), and Boltzmann statistics (statistics of a system of many identical, distinguishable particles, intermediate between the quantum mechanical Bose-Einstein and Fermi-Dirac statistics).
Contents |
[edit] Life
[edit] Youth
Ludwig Eduard Boltzmann was born to Ludwig Georg Boltzmann, tax officer, and Maria Pauernfeind, daughter of a well-to-do Salzburg merchant. Ludwig junior was baptized and raised as a Roman Catholic, the religion of his mother, while Ludwig senior was Protestant. The young Ludwig's elementary education took place under a private teacher in his parents’ home. Ludwig's parents were able to afford this, because the fairly modest civil servant salary of father Boltzmann was augmented by mother's fortune. Boltzmann senior was transferred regularly to different posts in the Austrian Empire. His last appointment was in Linz, where his son entered the Akademisches Gymnasium. Ludwig was a good student, with great interest in mathematics and science. In his spare time he took piano lessons (initially from the famous composer Anton Bruckner) and became an accomplished player. When Ludwig was fifteen years old he lost his father, who died of tuberculosis.
[edit] Student days in Vienna
In 1863 Boltzmann enrolled in the University of Vienna, where he majored in mathematics and physics. The university institute of physics had been founded just fourteen years earlier by Christian Doppler (1803–1854), the well-known discoverer of the Doppler effect. Already after three years (3 December 1866), Boltzmann received his doctorate (he had already published two papers) without writing a dissertation, because a formal thesis was not required at the University of Vienna before 1872–1873.
At Boltzmann's time, the institute of physics was directed by the Slovakia-born Jožef Stefan (1835–1893), who was later to become famous for his experimental discovery of the relation between black-body radiation and temperature T, what is now known as the Stefan-Boltzmann law (black-body radiation energy density is proportional to T 4 ). Stefan (who in the 1860s was around thirty, relatively young for a professor) had close contact with many of his students, among them Boltzmann. Many years later Boltzmann wrote in Stefan’s obituary the following:
When I deepened my contacts with Stefan, and I was still a university student at the time, the first thing he did was to hand me a copy of Maxwell’s papers and since at that time I did not understand a word of English, he also gave me an English grammar; I had received a dictionary from my father.
The fact that Stefan introduced Boltzmann around 1865 to the very recent work of James Clerk Maxwell on electromagnetic theory is remarkable, because Maxwell's work was then hardly known in the German speaking world.
After his doctorate Boltzmann became assistant to Stefan (1867) and in in 1868 he became "Privatdozent" (a person who is entitled to lecture). At that time he met Josef Loschmidt (1821–1895), who was Professor extraordinarius at the institute. Loschmidt, a generation older than Boltzmann, became his fatherly friend and exerted a lasting influence on him.
[edit] First stay in Graz
In 1869, at the miraculously young age of twenty-five, Boltzmann was called to the Karl-Franzens-Universität of Graz (Graz is today the second city of Austria) as full professor of mathematical physics. During the next few years Boltzmann took some short sabbaticals; he worked with the chemist Bunsen and the mathematician Königsberger in Heidelberg, and with the physicists Kirchhoff and Helmholtz in Berlin.
[edit] Professor of mathematics in Vienna
Boltzmann had a restless character and changed positions often. In 1873 he was offered a chair of mathematics in Vienna that he gladly accepted. Although Boltzmann was first and foremost a physicist, not a mathematician, the mathematics faculty in Vienna argued that Boltzmann's research is "excellent as mathematical works, containing solutions of very difficult problems of analytical mechanics and especially of probability calculus". They recognized "a decided mathematical talent" in his application of mathematical analysis to the theory of heat.
[edit] Marriage
While still in Graz, Boltzmann met his future wife, Henriette ("Jetty") von Aigentler (1854–1938), ten years his junior. After meeting him in 1873, she decided to start a study in mathematics at the university. One of her reasons was that she wanted to have some understanding and, if possible, some enthusiasm for her future husband's work. In the first semester Henriette was allowed to follow lectures, because there were no laws banishing women from university. But soon the Faculty approved a rule forbidding female students to attend lectures. Henriette presented a petition to the minister of public education for exemption from the new rule, which the minister granted her. However, when in the subsequent semester the problem arose again, she decided to give up on learning mathematics.
In a letter to Henriette dated September 27, 1875 Boltzmann proposed to her; he thought that it was proper make a marriage proposal in writing. It is not known whether she accepted by letter.
[edit] Second stay in Graz
Ludwig was working in Vienna at the time of his proposal, but the young couple had some misgivings about moving to Vienna: the housing and living were more expensive than in Graz and Jetty, who was from Graz, would be separated from her relatives. Very shortly after their engagement and before the wedding, a better position at the University of Graz became available. This was a chair in physics to which a laboratory was attached and Boltzmann wanted to extend his research to experimental physics. In addition, the administrative load in Graz would be less than in Vienna and also Boltzmann had still not found suitable housing in Vienna. Ludwig applied for the vacant position in Graz and around the time of the wedding (July 17, 1876), he heard that he was elected for the Graz chair.
The Boltzmanns spent the next fourteen years in Graz. They had two sons, Ludwig Hugo (1878–1889) and Arthur (1881–1952), and two daughters, Henriette (1880–1945) and Ida (1884–1910). A third daughter, Elsa (1891–1966), was born in Munich after the family had left Graz. During the fourteen years Boltzmann developed his ideas on the statistical conception of nature. His work was widely recognized and became honored and respected by the academic community and the government. The years of his second stay in Graz were the most fruitful and happy years in Boltzmann's life. In 1878 he became Dean of the Faculty and in 1887 Rector of Graz University. He became one of the great names in physics as is witnessed by his many invitations to memberships of scientific academies. At his death, Boltzmann was a member of the following academies: Göttingen, Vienna, Berlin, Stockholm, Uppsala, Turin, Rome, Amsterdam, St. Petersburg, New York, London, Paris, Washington, St. Louis; he received an honorary doctorate from Oxford University (1894).[2] He also received an H.C. doctorate from Clark University in Worcester (Massachusetts) while on tour in the USA.
Although a theoretician by heart, Boltzmann spent considerable effort in redoing Hertz’s experiments. These are documented in the last publication he wrote before leaving Graz. [3]
[edit] Years of depression
On 5 September 1906, Boltzmann hanged himself, while on vacation with his wife and youngest daughter Elsa in Duino, a village on the Adriatic sea, about 15 miles north of Trieste. Much has been speculated about the causes that drove Boltzmann to his suicide. Most likely, he suffered of a mental illness, then called neurasthenia, which is described as exhaustion of the central nervous system's energy reserves.
Boltzmann had a first mild nervous breakdown at the age of 41, after his mother died. He suffered a major psychological crisis between May and July of 1888, when he was rector of the university of Graz. The rector's responsibility for obligatory disciplinary measures against anti-Habsburg students (at that time the Austro-Hungarian Empire was ruled by the Habsburg emperor Franz-Joseph I) caused him much stress. Furthermore, it so happened that at the same time (early 1888) he was invited to succeed Gustav Kirchhoff at the University of Berlin. Although he initially accepted the very prestigious chair, after much soul-searching he broke his pledge and renounced the position. It is understandable that this decision gave him much tension and contributed greatly to his nervous breakdown in the early summer of 1888. It was then that his neurasthenia, his tendency to develop a manic-depressive syndrome, was diagnosed.
Boltzmann came out of this crisis as a worrier, he doubted his decisions and suffered anxieties about the importance of his position in the academic world. So he started to look for changes of place and university. The 1889 death of his son Ludwig (from a neglected appendicitis) must have been a damaging blow to him.
After he made it known that he wanted to leave Graz, Eugen Lommel, professor of experimental physics in Munich, obtained an appointment for Boltzmann to a chair of theoretical physics at the University of Munich. A chair of theoretical physics was a novelty, and the Munich faculty had to justify the change of a chair of (general) physics into one for theoretical physics only. However, they convinced the authorities and the Boltzmann family moved to Munich in the summer of 1890.
But, already in 1892, he began to feel homesick. In a letter to Loschmidt he writes that his life in Munich is OK, "but certainly not better than in dear old Austria". On 7 January 1893, his old supervisor at the University of Vienna, Jožef Stefan, died and his colleagues began maneuvers to have Boltzmann succeed him. In the spring of 1894 Boltzmann's choice between Munich and Vienna changed almost daily, until he accepted the appointment in Vienna, where he arrived in June 1894 as director of the physics institute.
Growing older, Boltzmann got physical problems as well. Already in Munich, his eyesight was deteriorating; mrs. Boltzmann read often scientific papers to her husband in order to spare his eyes. Furthermore his asthma was bothering him more and more. Notwithstanding his bad health he made three trips to the United States. In 1899 he traveled to New York and Massachusetts accompanied by his wife Henriette. In October 1904 Boltzmann participated in a meeting in St Louis and also visited Detroit and Chicago. In 1905, Boltzmann went for the last time to the United States, where he gave 30 lectures (in English) at a summer school held at the University of California in Berkeley. In Berkeley, the infamous San Francisco fog played havoc with his lungs, his asthma became really serious.
In 1895, Ernst Mach was appointed as Ordentlicher Professor der Philosophie, insbesondere für Geschichte und Theorie der induktiven Wissenschaften [ordinary professor of philosophy, in particular for the history and theory of the inductive sciences] at the University of Vienna and became a colleague of Boltzmann's. Although the two men did not fight openly, they were philosophical adversaries: Atomism against Energetics. Boltzmann soon realized that his return to Vienna was not a happy move. In letters to former colleagues in Munich he wrote that in Vienna there are "far fewer students ready for scientific work" than in Germany, and that his university offers little scientific stimulation. Nonetheless he wrote during these years a two-volume work that saw many reprints and of which the English translation is still available.[4]
Considering his complaints, it is no surprise that Boltzmann left Vienna again. He accepted in 1900 an appointment as Professor of Theoretical Physics in Leipzig, where the chemist Wilhelm Ostwald had built up a great research center. Although Ostwald as a person was a friend of Boltzmann’s, he was also the father of Energetics. Soon Boltzmann discovered that Leipzig, too, did not suit him. The scientific debate between the atomists and energeticists became so bitter that Mach himself thought that the argument was becoming too violent, and proposed a reconciliation of mechanistic and phenomenological physics.
After two years in Leipzig Boltzmann requested the Saxon government to release him for "reasons of health". Because his Viennese chair had remained vacant, he thought to go back to Vienna. However, the Austrian minister for education had a hard time silencing rumors circulating in Vienna, according to which Boltzmann was mentally ill. Nonetheless he was allowed to reoccupy his chair in 1902.
Boltzmann now lectured on theoretical physics at the University of Vienna and finished the second volume of his Lectures on the Principles of Mechanics. [5] In 1904, on the occasion of his 60th birthday, he was presented with a splendid Festschrift that was edited by his assistant Stefan Meyer (1872–1949) and comprised 117 contributions from the international community of physicists.[6]
After return from Berkeley, Boltzmann's depression deepened quickly and led to his suicide of 5 September 1906. Two days after his death Ernst Mach wrote in a Viennese newpaper[7]
Boltzmann had announced lectures for the summer semester of 1906, but had to cancel them, because of his nervous condition. In informed circles one knew that Boltzmann would most probably never be able to exercise his professorship again. One spoke of how necessary it was to keep him under constant medical surveillance, for he had already made earlier attempts at suicide.
[edit] Boltzmann's science
[edit] H theorem and entropy
In Graz, in 1872, Boltzmann published in the Sitzingsberichte der kaiserlichen Akademie der Wissenschaften in Wien (the Proceedings of the Imperial Academy of Sciences of Vienna, briefly "Wiener Berichte")[8] his celebrated H theorem. Boltzmann called it a "minimum theorem", and only later later it was christened by Samuel Burbury the "H-theorem" (H of heat). It is the first explicit probabilistic expression for the entropy of an ideal gas. Statistical methods applied to systems consisting of very many (say, more than 1020 ) atoms were introduced into physics by Maxwell in 1859; Boltzmann picked up Maxwell's ideas and carried them further.
Considering two-particle molecular collisions in a gas in the absence of external forces, he derived what is now known as the Boltzmann equation governing the time-development of the velocity distribution ft(v). The time t is written as a subscript to indicate that the distribution (a function of v) depends parametrically on time. Boltzmann introduced the H-functional
which is proportional to the negative of the equilibrium expression for the entropy S. Boltzmann showed that, if the distribution function ft is not the Maxwell-Boltzmann distribution at time t, the gas will evolve in such a way that H[ft ] decreases toward a time-independent minimum that is reached only when f takes the form of the Maxwell-Boltzmann distribution that describes an equilibrium:
In other words, the entropy function S = −H increases monotonically as the system approaches equilibrium.
The 1872 paper was based on a long-time definition of probability: if a system is in state S for a time period ts and the system evolves for a long time t then the probability that the system is in state S is equal to ts/t. Although Boltzmann employed probabilistic arguments, in 1872 he did not yet grasp the statistical character of entropy, he still believed that the second law is absolute and that it is impossible for entropy to decrease spontaneously.
[edit] The reversibility paradox
In 1876, Boltzmann’s 1872 paper encountered an objection from his friend Loschmidt.[9] Basically, Loschmidt's objection (the reversibility paradox) is that mechanical processes are reversible in time whereas most natural processes are not. Loschmidt points out that a time-reverted evolution of a mechanical system is obtained by taking the final state of a previous evolution as a new initial state followed by reversing all initial velocities of the atoms constituting the mechanical system. Then the evolution of the system runs backward in time. Of course, one never observes in reality any macroscopic, say biological, processes that are going backward in time.
In 1877 Boltzmann showed, in answer to his friend's objection, that the second law of thermodynamics formulated by Clausius and Thomson about two decades earlier ("in a spontaneous process entropy can only increase") is not absolute, but has a statistical origin. He published a landmark paper, [10] in which he formulated what Einstein later called the Boltzmann principle; the interpretation of the concept of entropy as a mathematically well-defined measure of what one can call the disorder of systems of atoms. Boltzmann showed that the irreversibility of natural processes is not absolute—not dictated by any mechanical law—but is caused by statistics. Time-reversion of, for instance, a biological process, although not impossible, is statistically so improbable that it will not be observed during the lifetime of the universe.
In his 1877 paper, Boltzmann introduced a new concept of probability that only holds close to equilibrium. He introduced finite cells in the phase space of an ideal gas consisting of many atoms. Using such cells to count the number of microstates (called Complexionen by Boltzmann, distributions of atoms over the cells), one can connect the number of possible microstates W (W from the German word Wahrscheinlichkeit meaning probability) with the entropy S of the given thermodynamic state. Boltzmann, considering atoms as identical, yet distinguishable, assigned discrete energies to them. Observe that the atoms of an ideal gas only possess kinetic energy.[11] The atoms have no a priori preference for any cell. Let there be ni atoms in cell i with energy εi, then
and the number W of microstates for a system in macrostate with given energy U is
This manner of counting, with identical distinguishable particles distributed over discrete cells, is now known as Boltzmann statistics. Assuming that equilibrium is the state of maximum probability, Boltzmann derived an equation for the entropy S. In the notation introduced later by Max Planck it reads
Here the Boltzmann constant kB appears.
[edit] The thermodynamics of black-body radiation
In 1879, Boltzmann's former supervisor Jožef Stefan concluded[12] from experimental evidence that the energy density (energy per unit volume) u(x, y, z) of black-body radiation in a cubic cavity is homogeneous, which means that everywhere in the cavity the energy density u is the same. Under this condition the total electromagnetic energy U of the cavity is equal to
Furthermore Stefan concluded that u is a function of absolute temperature T only. The density does not depend on the material or color of the walls of the cavity. From the data he was able to conjecture the expression (the law of Stefan-Boltzmann),
Here a is the radiation constant.[13]
In 1884 Boltzmann gave a derivation of this result.[14] He used the discovery of Maxwell that a beam of electromagnetic radiation that hits a wall perpendicularly gives radiation pressure u. (Note that pressure, force per unit surface, has the same dimension as energy per unit volume). Boltzmann realized that the beams that do not hit the wall perpendicularly give lower pressure. Suppose that a beam hits a wall of the cavity under an angle θ with the normal (that is, under an angle 90°−θ with the wall itself). Boltzmann assumed, in analogy to the pressure caused by atoms of an ideal gas, that the radiation pressure decreases proportional to cos2θ. In an ideal gas this dependence on θ is due to the fact that pressure is proportional to the square of the component along the normal of the velocity of the particles. If v is the velocity of an ideal gas particle then vn = v cosθ is the component of v along the normal, where v = |v|. The pressure in an ideal gas due to one particle is proportional to vn2 = v2cos2θ, hence Boltzmann's assumption of a cos2θ dependence. Further Boltzmann argues that the contribution from beams hitting a cavity wall between θ and θ+dθ is equal to sinθdθ. Because the incidence angle of the electromagnetic beams is between 0° and 90° (= π/2), he performs an integral over θ between these boundaries to obtain the total pressure p on the wall. Doing this he assumes that the density is isotropic (does not depend on angle), and he finds the simple relation between the electromagnetic pressure p in a cavity and the energy density u,
As a next step Boltzmann invokes thermodynamics. He uses a relation that he derived earlier in 1884 and that in modern form reads
Noting that U = u V and p = u/3, one readily obtains
from which
which is the result conjectured earlier by Stefan.
[edit] Atomism
For Boltzmann atoms were real mechanical entities, whereas his eminent colleague in Vienna, Ernst Mach professor of natural philosophy, did not believe in their existence at all. Mach saw an atom as an abstract tool to describe nature, similarly as a sine function describes the vibration of a string, but is not the actual vibration itself. Mach's doctrine came to be known as "Energetics", because according to Mach the only thing observable is exchange of energy. Energy is what we feel and measure; atoms are just fiction of imagination. Boltzmann's "atomism" was diametrically opposed to this standpoint.
The physical chemist Wilhelm Ostwald took openly the side of the energists when he addressed a meeting of the Deutsche Gesellschaft für Naturforscher und Ärzte [German Society for natural scientists and physicians] in 1895. He said
The proposition that all natural phenomena can ultimately be reduced to mechanical ones cannot even be taken as a useful working hypothesis: it is simply a mistake.
Ostwald then continued his speech by rehashing Loschmidt's old "reversibility paradox". A similar point of view was presented by Georg Helm, who spoke about "Energetics". Boltzmann reacted sharply. Fifty years later Arnold Sommerfeld, who was a young student at the time, gave an eye-witness report.[15]
The paper on Energetics was given by Helm from Dresden; behind him stood Wilhelm Ostwald, and behind both the natural philosophy of Ernst Mach, who was not present. The opponent was Boltzmann, seconded by Felix Klein. The battle between Boltzmann and Ostwald resembled the battle of the bull with the supple fighter. However, this time the bull defeated the torero in spite of his fighting art. The arguments of Boltzmann struck home. We, the young mathematicians of the time, were all on the side of Boltzmann; it was immediately obvious to us that one could not possibly deduce the equation of motion for even a single mass point—let alone for a system with an arbitrary number of degrees of freedom—from the energy equation.
Nowadays nobody doubts the existence of atoms anymore, Boltzmann's view has been completely vindicated by many later discoveries. For instance, the 1986 Nobel prize in physics was awarded for the scanning tunneling microscope, an instrument by which one can observe individual atoms directly.
[edit] Notes and references
- ↑ The present article is partly based on the following sources:
- Carlo Cercignani and Roger Penrose, Ludwig Boltzmann: The Man Who Trusted Atoms, Oxford University Press (2006). Restricted access.
- Wolfgang L. Reiter, In Memoriam Ludwig Boltzmann: A Life of Passion, Physics in perspective, vol. 9 pp. 357–374 (2007) Restricted access
- Carlo Cercignani and Roger Penrose, Ludwig Boltzmann: The Man Who Trusted Atoms, Oxford University Press (2006). Restricted access.
- ↑ From A. Sommerfeld, Allgemeine deutsche Biographie & Neue deutsche Biographie: Biographie Boltzmann. (Retrieved 12/19/2011).
- ↑ L. Boltzmann, Über die Hertzschen Versuche [About the experiments of Hertz], Annalen der Physik, vol. 276, pp. 399–400 (1890)
- ↑ L. Boltzmann (1895–8). Vorlesungen Über Gastheorie, 2 vols., J. A. Barth, Leipzig. Lectures on Gas Theory, Dover Books on Physics, (1995)
- ↑ L. Boltzmann, Vorlesungen über die Principe der Mechanik. 2 Vols., J. A. Barth, Leipzig 1904).
- ↑ S. Meyer, ed., Festschrift Ludwig Boltzmann gewidmet zum sechzigsten Geburtstage 20. Februar 1904. Leipzig: J. A. Barth, 1904. Online
- ↑ E. Mach Ludwig Boltzmann, Die Zeit (Vienna), no. 1420, Abendblatt p. 1, 7 September (1906).
- ↑ L. Boltzmann, Weitere Studien über die Wärmegleichgewicht unter Gasmolekülen [Further studies on the thermal equilibrium among gas molecules], Wiener Berichte II, vol. 66, pp. 275–370 (1872); presented October 10, 1872.
- ↑ J.Loschmidt, Über den Zustand des Wärmegleichgewichtes eines Systems von Körpern mit Rücksicht auf die Schwerkraft [On the state of the heat equilibrium of a system of bodies with consideration of the gravitational force], Wiener Berichte II, vol. 73, pp. 128–142 (1876)
- ↑ L. Boltzmann, Über die Beziehung zwischen dem zweiten Hauptsatze des mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung, respective den Satzen uber das Wärmegleichgewicht [On the relation between the second law of the mechanical theory of heat and the probability calculus with respect to theorems of thermal equilibrium] Wiener Berichte II, vol. 76, pp. 373-435 (1877)
- ↑ It is of interest to point out that Boltzmann still used the German equivalent lebendige Kraft (live force) for Leibniz's term vis viva for kinetic energy.
- ↑ J. Stefan, Über die Beziehung zwischen der Wärmestrahlung und der Temperatur [On the relation between the heat radiation and temperature], Wiener Berichte II, vol. 79 pp. 391-428 (1879).
- ↑ The modern numeric value of a is 7.565731 × 10−16 J m−3 K−4. From NIST CODATA (retrieved 12/20/2011). The closely related constant σ = c/(4a) is the Stefan-Boltzmann constant (c is the speed of light).
- ↑ L. Boltzmann, Ableitung des Stefanschen Gesetzes, betreffend die Abhängigkeit der Wärmestrahlung von der Temperatur aus der electromagnetischen Lichttheorie [Derivation of Stefan's law regarding the dependence of heat radiation on temperature from the electromagnetic theory of light], Annalen der Phyik, vol. 22, pp. 291–294 (1884) DOI
- ↑ A. Sommerfeld, Das Werk Boltzmanns, Wiener Chemiker Zeitung February 1944 nr. 3/4 p. 25 vol 47.
[edit] External links
- Encyclopedia.com From: Complete Dictionary of Scientific Biography (2008)
- Stanford Encyclopedia of Philosophy J. Uffink, Boltzmann's work in statistical physics (2004)






![H[f_t] := \int f_t(\mathbf{v}) \ln f_t(\mathbf{v}) d^3\mathbf{v},](../w/images/math/f/2/4/f240a32b5f3e96532a7f0fa40f0f17e0.png)
![\frac{d H[f_t]}{dt} \le 0, \qquad f = Ae^{Bv^2}\;\Longrightarrow\; \frac{d H[f_t]}{dt} = 0 .](../w/images/math/1/b/9/1b94d94d741e78d019c381259ee1e09c.png)


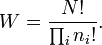
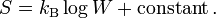
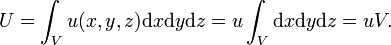
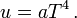
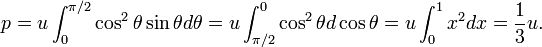
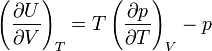
![u = \frac{1}{3} \left[ T \frac{d u}{d T} - u\right]
\rightarrow \frac{d u}{u} = 4 \frac{dT}{T} \rightarrow
\ln\left(\frac{u}{u_0}\right) = \ln\left( \frac{T}{T_0} \right)^4,](../w/images/math/0/a/5/0a544dbf9ba73ffb0ac8be9103408fac.png)