Black-body radiation
A black body absorbs and then re-emits all incident EM radiation. By definition it has an absorptivity and emissivity of 1, and a transmissivity and reflectivity of 0. The Planck Black Body equation describes the spectral exitance of an ideal black body. The study of black-body radiation was an integral step in the formulation of quantum mechanics.
Contents |
[edit] Planck's Law: Wavelength
Formulated in terms of wavelength:
![M(\lambda,T) [\frac{W}{m^2 m}] = \frac{ 2 \pi h c^2 }{ \lambda^5 ( \exp^{\frac{h c}{\lambda K T}} - 1 ) }](../w/images/math/8/b/d/8bdcc7d42f2fa1f4f5b31527c33449ed.png)
where:
| Symbol | Units | Description |
|---|---|---|
| λ | [m] | Input wavelength |
| T | [K] | Input temperature |
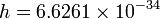
|
[J * s] | Planck's constant |
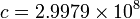
|
![[\frac{m}{sec}]](../w/images/math/6/b/8/6b8693dfb105752676fe7fbae620ad9e.png)
|
Speed of light in vacuum |
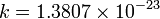
|
[erg * K] | Boltzmann constant |
Note that the input λ is in meters and that the output is a spectral irradiance in [W / m2 * m]. Omitting the π term from the numerator gives the blackbody emission in terms of radiance, with units [W / m2 * sr * m] where "sr" is steradians.
[edit] Planck's Law: Frequency
Formulated in terms of frequency:
![M(v,T) [\frac{W}{m^2 Hz}] = \frac{ 2 \pi h v^3 }{ c^2 ( \exp^{\frac{h c}{K T}} - 1 ) }](../w/images/math/2/e/3/2e3fa629add159727545747894c2035b.png)
where:
| Symbol | Units | Description |
|---|---|---|
| v | [Hz] | Input frequency |
All other units are the same as for the Wavelength formulation. Again, dropping the π from the numerator gives the result in radiance rather than irradiance.
[edit] Properties of the Planck Equation
Taking the first derivative leads to the wavelength with maximum exitance. This is known as the Wien Displacement Law.
A closed form solution exists for the integral of the Planck blackbody equation over the entire spectrum. This is the Stefan-Boltzmann equation. In general, there is no closed-form solution for the definite integral of the Planck blackbody equation; numerical integration techniques must be used.[1][2]
The relationship between the ideal blackbody exitance and the actual exitance of a surface is given by emissivity.
An ideal blackbody at 300K (~30 Celsius) has a peak emission 9.66 microns. It has virtually no self-emission before 2.5 microns, hence self-emission is typically associated with the "thermal" regions of the EM spectrum. However, the Sun can be characterized as a 5900K blackbody and has a peak emission around 0.49 microns which is in the visible region of spectrum.
The Planck equation has a single maximum. The wavelength with peak exitance becomes shorter as temperature increases. The total exitance increases with temperature.
[edit] Citations
- ↑ Paez, G. and Strojnik, M. "Integrable and differentiable approxiations to the generalized Planck's equations." Proceedings of SPIE. Vol 3701, pp 95-105. DOI=10.1117/12.352985
- ↑ Lawson, Duncan. "A closer look at Planck's blackbody equation." Physics Education 32.5 (Sept. 1997): 321-326. IOP. 19 Sept. 2007 <http://stacks.iop.org/0031-9120/32/321>.
| |
Some content on this page may previously have appeared on Citizendium. |

