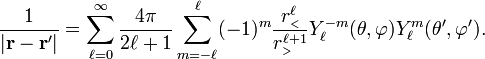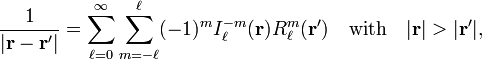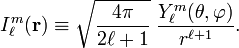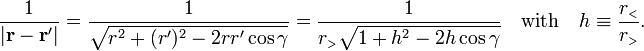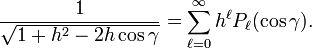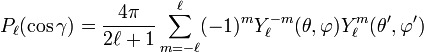Laplace expansion (potential)
In physics, the Laplace expansion of a 1/r - type potential is applied to expand Newton's gravitational potential or Coulomb's electrostatic potential. In quantum mechanical calculations on atoms the expansion is used in the evaluation of integrals of the interelectronic repulsion.
[edit] The expansion
The Laplace expansion is in fact the expansion of the inverse distance between two points. Let the points have position vectors r and r', then the Laplace expansion is
Here r has the spherical polar coordinates (r, θ, φ) and r'
has ( r', θ', φ').
Further r<
is min(r, r')
and r> is max(r, r').
The function 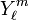 is a normalized spherical harmonic function. The expansion takes a simpler form when written in terms of solid harmonics,
is a normalized spherical harmonic function. The expansion takes a simpler form when written in terms of solid harmonics,
where 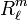 is a regular solid harmonic:
is a regular solid harmonic:
and 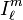 is an irregular solid harmonic:
is an irregular solid harmonic:
[edit] Derivation
The derivation of this expansion is simple. One writes
We find here the generating function of the Legendre polynomials 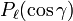 :
:
Use of the spherical harmonic addition theorem
gives the desired result.