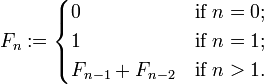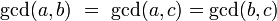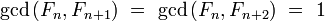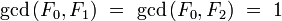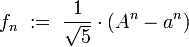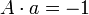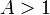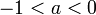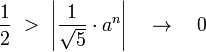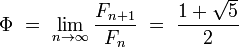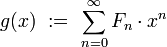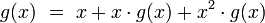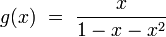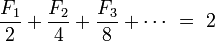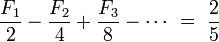Fibonacci number
In mathematics, the Fibonacci numbers form a sequence in which the first number is 0, the second number is 1, and each subsequent number is equal to the sum of the previous two numbers in the series. In mathematical terms, it is defined by the following recurrence relation:
The sequence of Fibonacci numbers starts with : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...
It was first used to represent the growth of a colony of rabbits, starting with a single pair of rabbits. It has applications in mathematics as well as other sciences, and is a popular illustration of recursive programming in computer science.
Contents |
[edit] Divisibility properties
We will apply the following simple observation to Fibonacci numbers:
if three integers 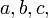 satisfy equality
satisfy equality 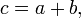 then
then
where "gcd" denotes the greatest common divisor.
Indeed,
and the rest is an easy induction.
- for all integers
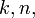 such that
such that 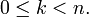
Indeed, the equality holds for 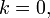 and the rest is a routine induction on
and the rest is a routine induction on 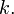
Next, since 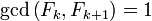 , the above equality implies:
, the above equality implies:
which, via Euclid algorithm, leads to:
Let's note the two instant corollaries of the above statement:
- If
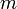 divides
divides 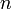 then
then 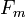 divides
divides 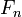
- If
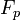 is a prime number different from 3, then
is a prime number different from 3, then 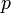 is prime. (The converse is false.)
is prime. (The converse is false.)
[edit] Algebraic identities
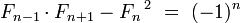 for n=1,2,...
for n=1,2,...
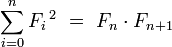
[edit] Direct formula and the golden ratio
We have
for every 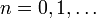 .
.
Indeed, let 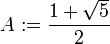 and
and 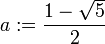 . Let
. Let
Then:
-
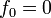 and
and 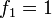
-
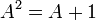 hence
hence 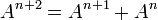
-
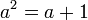 hence
hence 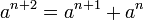
-
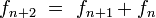
for every 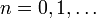 . Thus
. Thus 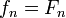 for every
for every 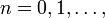 and the formula is proved.
and the formula is proved.
Furthermore, we have:
It follows that
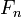 is the nearest integer to
is the nearest integer to 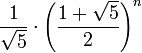
for every 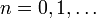 . The above constant
. The above constant 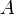 is known as the famous golden ratio
is known as the famous golden ratio  Thus:
Thus:
[edit] Fibonacci generating function
The Fibonacci generating function is defined as the sum of the following power series:
The series is convergent for 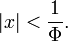 Obviously:
Obviously:
hence:
Value 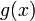 is a rational number whenever x is rational. For instance, for x = ½:
is a rational number whenever x is rational. For instance, for x = ½:
and for x = −½ (after multiplying the equality by −1):
[edit] Further reading
- John H. Conway and Richard K. Guy, The Book of Numbers, ISBN 0-387-97993-X
| |
Some content on this page may previously have appeared on Citizendium. |