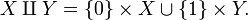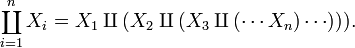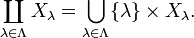Disjoint union

From Knowino

Pending changes are displayed on this page

Unchecked

Jump to: navigation, search

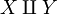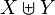In mathematics, the disjoint union of two sets X and Y is a set which contains disjoint (that is, non-intersecting) "copies" of each of X and Y: it is denoted $X \amalg Y$ or, less often, $X \uplus Y$ .

There are injection maps in₁ and in₂ from X and Y to the disjoint union, which are injective functions with disjoint images.

If X and Y are disjoint, then the usual union is also a disjoint union. In general, the disjoint union can be realised in a number of ways, for example as

$X \amalg Y = \{0\} \times X \cup \{1\} \times Y . \,$

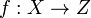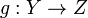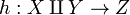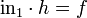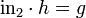The disjoint union has a universal property: if there is a set Z with maps $f:X \rightarrow Z$ and $g:Y \rightarrow Z$ , then there is a map $h : X \amalg Y \rightarrow Z$ such that the compositions $\mathrm{in}_1 \cdot h = f$ and $\mathrm{in}_2 \cdot h = g$ .

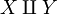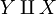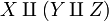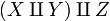The disjoint union is commutative, in the sense that there is a natural bijection between $X \amalg Y$ and $Y \amalg X$ ; it is associative again in the sense that there is a natural bijection between $X \amalg (Y \amalg Z)$ and $(X \amalg Y) \amalg Z$ .