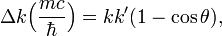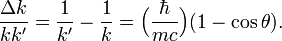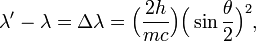Compton effect
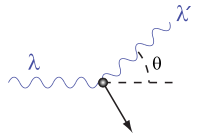
The Compton effect is the scattering of an X-ray photon off a free, or nearly free, electron. During the scattering some energy of the photon is transferred to the electron with the consequence that the wavelength λ′ of the scattered X-rays is longer by an amount Δλ than of the incident X-rays. Noteworthy is the fact the energy transfer depends on the angle θ between the incident and scattered ray:
where h is Planck's constant, m is the rest mass of the electron and c is the speed of light. The Compton effect showed for the first time that the photon has a momentum with a well-defined direction, a vector. The quantity h/(mc) is known as the Compton wavelength of the electron; it is equal to 2.43×10−12 m.
The scattering was observed and theoretically explained in 1922[1] by Arthur Holly Compton (1892-1962) who gave his name to the effect. Already in 1905 Albert Einstein had proposed that electromagnetic radiation, such as X-rays, consists of energy parcels (photons). Compton's work showed that (X-ray) photons not only have energy, but also momentum, just like ordinary (nonzero rest mass) particles. It was known since the 19th century that visible light consists of waves. Later it was shown that this holds for electromagnetic radiation of all wavelengths, including X-rays. Compton's observation implies that light can be seen as a stream of corpuscles as well in agreement with Isaac Newton's view (ca. 1680). The particle and wave points of view being simultaneously true is known as wave-particle duality.
Compton received the Nobel in Physics in 1927 for "his discovery of the effect named after him."[2] His discovery came almost simultaneous with the discovery of Louis de Broglie that particles, such as electrons, have wave character. Electrons having wave character is also a form of wave-particle duality.
[edit] Derivation of equation (1)
The derivation of equation (1) by Compton predates the new quantum mechanics of Heisenberg, Schrödinger, Dirac and others. It is, however, based on Einstein's theory of special relativity. Without knowing about the uncertainty relation between momentum and position, Compton considers a free electron at rest positioned at certain point in space.[3] The electron is hit by a photon of momentum ℏk, where k is the wave vector and ℏ is Planck's constant divided by 2π,
and λ is the wavelength of the incident light. After scattering the photon has wave vector k′ and wavelength λ′. The energy of the incident photon is ℏck, where c is the speed of light.
A relativistic particle, such as an electron, with velocity v and rest mass m has kinetic energy E and momentum p,
Before scattering the electron has velocity v = 0 and hence energy mc2 and momentum p = 0. After scattering it has non-zero velocity v and corresponding energy and momentum. It is convenient to express the energy E in terms of p (the modulus of p).
so that the relativistic energy of a particle with rest mass m and magnitude of momentum p is,
Compton's derivation is based on two conservation laws. (I) Conservation of momentum (a vector equation):
and (II) conservation of energy. Noting that v = 0 gives p = 0 and E = mc2, one has the energy (scalar) equation with on the left-hand side the energy of the system (electron plus photon) before scattering and on the right-hand side the energy of the system after scattering:
From (I)
where θ is the scattering angle. Introduce Δk := k−k′ so that
Substitute this into (II) and divide through by cℏ,
Bring mc/ℏ to the left-hand side and square the equation,
This yields
from which
Multiply by 2π and use that (1-cosθ) = 2 (sinθ/2)2
which proves Compton's equation.
Note that conservation law (I) (conservation of momentum) is a landmark equation in the history of physics. In 1922, when Compton performed his derivation, most physicists did not believe that photons were particles, they saw them parcels of energy and not more than that. Compton made a great stride by associating a momentum vector with a light quantum, a vector with a distinct direction, like all moving particles possess. Further he assumed that this photon momentum plays the usual role in an elastic (total energy conserved) scattering of a photon and electron.
As pointed out above, Compton's assumption of a free electron in an eigenstate of the momentum operator (with zero eigenvalue) means quantum mechanically that the position of the electron is completely undetermined. Shortly after the advent of the new quantum mechanics, Compton scattering was reconsidered from a quantum mechanical viewpoint, see for instance Ref.[4] and Ref.[5]
[edit] References
- ↑ A. H. Compton, A Quantum Theory of the Scattering of X-rays by Light Elements, Physical Review, vol. 21, pp. 483–502 (1923) DOI
- ↑ Nobel Prize in Physics 1927 Nobel Foundation
- ↑ In the new quantum mechanics an electron at rest is in an eigenstate of momentum and has an equal probability of being anywhere in space.
- ↑ W. Gordon, Der Comptoneffekt nach der Schrödingerschen Theorie [The Compton effect according to Schrödinger's theory] Zeitschrift für Physik, Volume 40, pp. 117-133, DOI
- ↑ O. Klein and Y. Nishina, Über die Streuung von Strahlung durch freie Elektronen nach der neuen relativistischen Quantendynamik von Dirac [On the scattering of radiation by free electrons according to the new relativistic quantum dynamics of Dirac], Zeitschrift für Physik, Volume 52, pp. 853-868, DOI
[edit] External links
- The Compton Effect Andrew Duffy (2000). Boston University, Physics Department
- Compton Scattering Rod Nave. Hyper Physics, Georgia State University



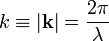
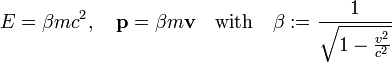
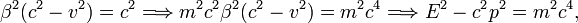


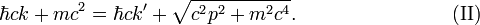
![p^2 = \hbar^2\left[ k^2 + (k')^2 - 2 kk'\cos\theta\right]](../w/images/math/f/e/a/fea0f2c80780776d3fb0e16057c9374b.png)
![c^2 p^2 = (c\hbar )^2 \left[ (\Delta k)^2 +2 kk' - 2 kk'\cos\theta\right]
= (c\hbar)^2 \left[ (\Delta k)^2 +2 kk'(1-\cos\theta)\right]](../w/images/math/9/8/f/98f29e19a233dd82bc45fd06c3f795c9.png)
![\Delta k = \sqrt{ \left[ (\Delta k)^2 +2 kk'(1-\cos\theta)\right]
+ \Big(\frac{mc}{\hbar }\Big)^2} - \Big(\frac{mc}{\hbar}\Big)](../w/images/math/3/8/0/380fbacc71d84744474017c7d0a7aef2.png)
![\left[ \Delta k + \Big(\frac{mc}{\hbar}\Big)\right]^2
= (\Delta k)^2 +2 kk'(1-\cos\theta)+ \Big(\frac{mc}{\hbar }\Big)^2](../w/images/math/1/7/4/174dfba60cab0cf272b1335be5775bfe.png)