Circle (mathematics)
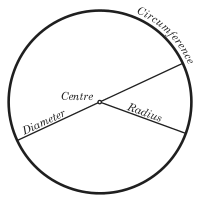
In geometry, the term circle has two closely related meanings. In its first meaning it is a set of points in a two-dimensional Euclidean space (a plane) bounded by one curved line, called the circumference of the circle. In this meaning a circle consists of interior points and points on the boundary, the circumference. The circumference is such that all its points have the same distance from a certain fixed point in the circle, the center of the circle.
In the second meaning of the term, the circumference only is indicated by circle (e.g., "draw a circle through three points"). It is always possible to tell from the context which of the two meanings is intended.
Any straight line segment, passing through the center and on both extremities terminated by the circumference, is called a diameter of the circle. From the definition of the circle follows immediately that all diameters have the same length. This common length is referred to as the diameter of the circle; it measures the size of the circle. Hence, the term diameter also has two meanings: (i) a line segment and (ii) the length of the line segment. A radius of a circle is any line joining the center to a point on the circumference. All radii have the same length called the radius of the circle. Obviously the radius is half the diameter of a circle. Finally, the term circumference has also two meanings: (i) a curved line bounding a circle and (ii) the length of this curved line.
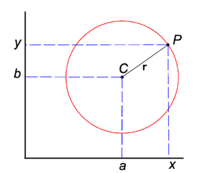
The circle is one of the four conic sections. The points on its circumference are represented algebraically by
- (x − a)2 + (y − b)2 = r2
where the circle's center has the cartesian coordinates (a,b); an arbitrary point P on the circumference has coordinates (x, y); the radius is the length r; see Fig. 2. Note that the equation for the circle (in its second meaning as curved line) is simply an application of the Pythagorean theorem.
In the complex plane ℂ a circle (in its first meaning) is represented by the locus of points z ∈ ℂ that satisfies the equation 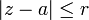 . Here the circle has center a ∈ ℂ and radius r ∈ ℝ.
. Here the circle has center a ∈ ℂ and radius r ∈ ℝ.
The transcendental number π is defined as the ratio of the circumference (length) c and diameter (length) d of an arbitrary circle, π := c/d. Or: the circumference c of a circle is equal to 2πr, where r = d/2 (radius of a circle is half its diameter). A given circle of radius r has area πr 2.