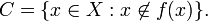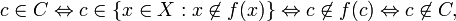Cantor's diagonal argument
Cantor's diagonal argument provides a convenient proof that the set 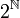 of subsets of the natural numbers (also known as its power set) is not countable. More generally, it is a recurring theme in computability theory, where perhaps its most well known application is the negative solution to the halting problem.
of subsets of the natural numbers (also known as its power set) is not countable. More generally, it is a recurring theme in computability theory, where perhaps its most well known application is the negative solution to the halting problem.
[edit] Informal description
The original Cantor's idea was to show that the family of 0-1 infinite sequences is not countable. This is done by contradiction. If this family is countable then its members can be enumerated or enlisted. Such a list gives a table of digits, like in the following arbitrarily chosen example:
- 0, 1, 0, 1, 0, ...
- 1, 1, 1, 1, 0, ...
- 1, 0, 1, 0, 0, ...
Now, we construct a sequence s = (s1, s2, s3, ....), which is not on the list while still, 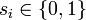 for all i. This is done as follows. Take s1 to be different from the first digit of the first member on the list. In our example the digit is 0 (in boldface) and so s1 is defined to be 1. Take s2 to be different from the second digit of the second member on the list (in our example s2 = 0). Generally, define sn as different from the n-th digit of the n-th entry on the list. In other words, the sequence s = (s1, s2, s3, ....) contains "the complement in {0,1}" of the diagonal of our table. It follows that that the sequence s itself is not on the list, since it is different from every member by the definition. The list was supposed to contain all the 0-1 sequences. The contradiction shows that such sequences can not be enumerated (or they are not countable).
for all i. This is done as follows. Take s1 to be different from the first digit of the first member on the list. In our example the digit is 0 (in boldface) and so s1 is defined to be 1. Take s2 to be different from the second digit of the second member on the list (in our example s2 = 0). Generally, define sn as different from the n-th digit of the n-th entry on the list. In other words, the sequence s = (s1, s2, s3, ....) contains "the complement in {0,1}" of the diagonal of our table. It follows that that the sequence s itself is not on the list, since it is different from every member by the definition. The list was supposed to contain all the 0-1 sequences. The contradiction shows that such sequences can not be enumerated (or they are not countable).
The role of the diagonal clearly explains the name of the argument.
[edit] Formal argument
To prove that the family of all subsets of 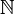 is not countable, we associate to any set
is not countable, we associate to any set 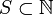 its characteristic function
its characteristic function 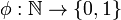 by setting
by setting 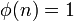 if
if 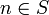 and
and 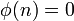 , otherwise. Conversely, every such function defines a subset. Observe also that every such function corresponds to a 0-1 sequence and vice-versa.
, otherwise. Conversely, every such function defines a subset. Observe also that every such function corresponds to a 0-1 sequence and vice-versa.
If power set is countable, there is a bijective map 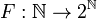 , that allows us to assign an index i = F − 1(S) to every subset S. In other words, all the functions
, that allows us to assign an index i = F − 1(S) to every subset S. In other words, all the functions 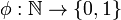 can be enumerated as
can be enumerated as 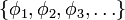 . Assuming this has been done, we proceed to construct a function
. Assuming this has been done, we proceed to construct a function 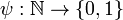 that is not in this list. Consequently, the corresponding set, T cannot be in the range of F.
that is not in this list. Consequently, the corresponding set, T cannot be in the range of F.
For each i, either 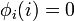 or
or 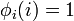 , and so we define
, and so we define 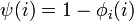 . Clearly,
. Clearly, 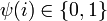 and
and 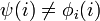 .
.
It follows that 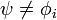 for any i, and it must therefore correspond to a set not in the range of F. This contradiction shows that
for any i, and it must therefore correspond to a set not in the range of F. This contradiction shows that 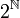 cannot be countable.
cannot be countable.
[edit] Application to general sets
More generally, the argument shows that a set cannot be put into one-to-one correspondence with its power set: equivalently, the cardinality of a set is strictly less than that of its power set. The argument proceeds by showing that there cannot be a surjection from a set X to the set PX of subsets of X. Suppose if possible that there were such a surjection f. Form the set
Since C is a subset of X then from the assumption that f is surjective there is an element c of X such that f(c) = C. We now ask whether c is in C. We find that
which is a contradiction. Hence the supposition that f is a surjection is untenable. In particular, then, f cannot be a bijection.
| |
Some content on this page may previously have appeared on Citizendium. |