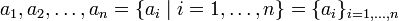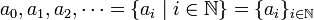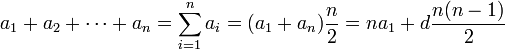Arithmetic sequence
From Knowino
This is a pending revision of this page. It may differ from the latest accepted revision, which was accepted on 14 January 2011.
An arithmetic sequence (or arithmetic progression) is a (finite or infinite) sequence of (real or complex) numbers such that the difference of consecutive elements is the same for each pair.
Examples for arithmetic sequences are
- 2, 5, 8, 11, 14, 17 (finite, length 6: 6 elements, difference 3)
- 5, 1, −3, −7 (finite, length 4: 4 elements, difference −4)
- 1, 3, 5, 7, 9, ... (2n − 1), ... (infinite, difference 2)
[edit] Mathematical notation
A finite sequence
or an infinite sequence
is called arithmetic sequence if
- ai + 1 − ai = d
for all indices i. (The index set need not start with 0 or 1.)
[edit] General form
Thus, the elements of an arithmetic sequence can be written as
- ai = a1 + (i − 1)d
[edit] Sum
The sum (of the elements) of a finite arithmetic sequence is
| |
Some content on this page may previously have appeared on Citizendium. |