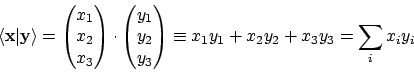 |
(13) |
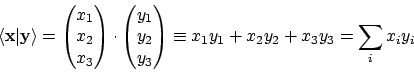 |
(13) |
p = x'*yMerk op dat het inproduct tussen complexe vectoren gedefinieerd is als
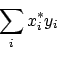 |
(14) |
x'*y doet.
De norm (ook wel lengte) van een vector is gedefinieerd
door
| (15) |
norm gebruiken:
norm(x)-sqrt(x'*x)of je kunt zelf de som van de kwadraten uitrekenen met
sum(x.^2)Let op:
length(x)geeft het aantal elementen van een vector (3 in dit geval). De afmetingen van een matrix krijg je overigens met
size(A)
De hoek ![]() tussen twee vectoren
tussen twee vectoren ![]() en
en ![]() is impliciet gedefinieerd door
is impliciet gedefinieerd door
| (16) |
We kunnen nu ook de projectie (![]() )
van de vector
)
van de vector ![]() op
op
![]() uitrekenen. Per definitie is dit een vector die
te schrijven is als
uitrekenen. Per definitie is dit een vector die
te schrijven is als
![]() zodanig dat
de vector
zodanig dat
de vector
![]() loodrecht staat op
loodrecht staat op ![]() (maak voor jezelf een schetsje maakt met al de genoemde vectoren).
Leidt een formule af voor
(maak voor jezelf een schetsje maakt met al de genoemde vectoren).
Leidt een formule af voor ![]() .
Reken nu met MATLAB de vectoren
.
Reken nu met MATLAB de vectoren ![]() en
en ![]() uit en controleer of de
laatste inderdaad loodrecht staat op
uit en controleer of de
laatste inderdaad loodrecht staat op ![]() .
.
De formule wordt iets eenvoudiger als je eerst de vector
![]() normeert:
normeert:
| N | = | (17) | |
| = | (18) |
| (19) |
Het vlak V opgespannen door de vector ![]() en
en ![]() is
de verzameling van alle vectoren die kunnen worden
geschreven als een lineaire combinatie van deze twee vectoren.
Een orthonormale basis
is
de verzameling van alle vectoren die kunnen worden
geschreven als een lineaire combinatie van deze twee vectoren.
Een orthonormale basis
![]() voor het vlak Vbestaat uit twee genormeerde vectoren in V die onderling loodrecht staan.
Maak zo'n basis (hint: de vector
voor het vlak Vbestaat uit twee genormeerde vectoren in V die onderling loodrecht staan.
Maak zo'n basis (hint: de vector ![]() is een mooi begin,
lees verder de definitie van projectie nog eens goed).
is een mooi begin,
lees verder de definitie van projectie nog eens goed).
De vector ![]() kan geschreven worden in de basis
kan geschreven worden in de basis ![]()
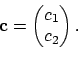 |
(21) |
Met welk MATLAB statement kun je in één keer de expansiecoefficiënten
van zowel ![]() als
als ![]() in de basis
in de basis ![]() berekenen?
berekenen?
Laat zien dat de lengte van ![]() gelijk is aan
gelijk is aan
![]() door vgl. 20 in te vullen in
door vgl. 20 in te vullen in
| (22) |
Bereken de componenten b1 en b2 van de vector
![]() (vlg. 4) in de basis
(vlg. 4) in de basis ![]() .
Vergelijk
.
Vergelijk
![]() met
met
![]() .
Wat is hier
aan de hand?
.
Wat is hier
aan de hand?
Bereken de projectie ![]() van de vector
van de vector ![]() op het vlak V.
op het vlak V.
Wat is de afstand van ![]() tot V?
tot V?
Het zou nu duidelijk moeten zijn waarom het stelsel
x = [ a1 a2 ] \ bgeeft, krijg je toch een antwoord. Om te begrijpen wat dit antwoord betekent vullen we
z = [ a1 a2 ] * xVergelijk
| (24) |
De vector ![]() en de matrix
en de matrix ![]() zijn gegeven door
zijn gegeven door
| (27) |
det(D)).
Beschouw het lineaire stelsel
| (29) |
Hoe kun je controleren of je het goede antwoord voor ![]() hebt gevonden?
hebt gevonden?