Next: Inproduct en norm
Up: Matlab instructie
Previous: MATLAB scripts
Gegeven zijn de vier vectoren:
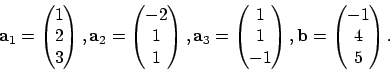 |
(4) |
Gevraagd is: welke lineaire combinatie van de
vectoren
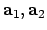 en
en 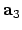 is gelijk
aan de vector
is gelijk
aan de vector 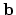 ,
oftewel, los op:
,
oftewel, los op:
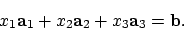 |
(5) |
Dit lineaire stelsel kan herschreven worden als
In MATLAB kun je dit stelsel oplossen met
x = A\b
Als de inverse van 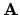 bestaat, d.w.z.,
bestaat, d.w.z., 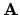 is een
vierkante matrix waarvan de determinant ongelijk aan
nul is [MATLAB commando:
is een
vierkante matrix waarvan de determinant ongelijk aan
nul is [MATLAB commando: det(A)], kun je de oplossing
ook schrijven als
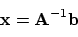 |
(8) |
en in MATLAB wordt dit
x = inv(A) * b
In MATLAB is de methode met de backslash (\) het
beste (iets nauwkeuriger en iets sneller). Let op:
de forward slash (/) doet net iets anders:
C=A/B
is de ``betere manier'' om
C=A*inv(B)
uit te rekenen. In een enkel geval wil je helemaal geen
lineair stelsel oplossen, maar, voor twee matrices
A en B die dezelfde afmetingen hebben
ieder element van A delen door een element van
B:
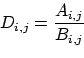 |
(9) |
Dit doe je in MATLAB met
D = A./B
Voor matrix vermenigvuldiging is de situatie analoog:
C = A * B
is een matrix vermenigvuldiging:
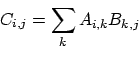 |
(10) |
terwijl
D = A .* B
een zogenaamde puntsgewijze vermenigvuldiging is:
De zogenaamde standaard basis voor 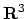 bestaat uit
de drie vectoren
bestaat uit
de drie vectoren
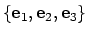
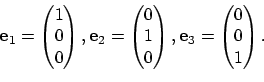 |
(12) |
Als je deze vectoren naast elkaar zet krijg je de
eenheidsmatrix. In MATLAB heb je daarvoor het commando
E = eye(3)
Van het vak lineaire algebra weet je misschien nog
de regel: ``de kolommen van een matrix zijn de
beelden van de basisvectoren''. Probeer te voorspellen
wat hier uit komt:
e2 = E(:,2)
d = A(:,2) - A*e2
Met de volgende commandos kun je een matrix of vector met
allemaal nullen respectievelijk allemaal enen maken:
zeros(3) % 3x3 matrix met nullen
ones(3) % 3x3 matrix met enen
ones(3,1) % kolom vector met enen
zeros(1,3) % rijvector met nullen
Wat ook handig kan zijn:
D = diag([2 3 -1]) % diagonaal matrix met gegeven elementen
d = diag(D) % stop diagonaal elementen weer in een vector
Bedenk een alternatief voor het commando eye(17)




Next: Inproduct en norm
Up: Matlab instructie
Previous: MATLAB scripts
Gerrit Groenenboom
2002-09-05
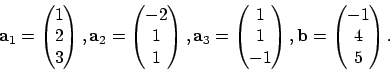
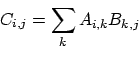
![]() bestaat uit
de drie vectoren
bestaat uit
de drie vectoren
![]()