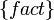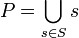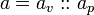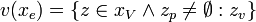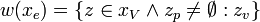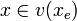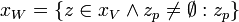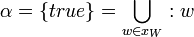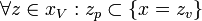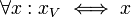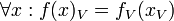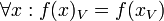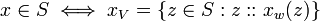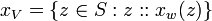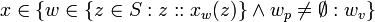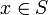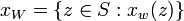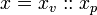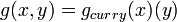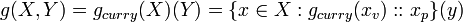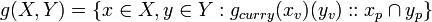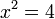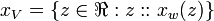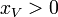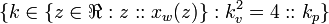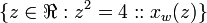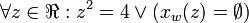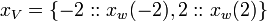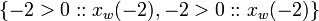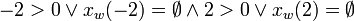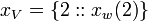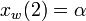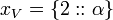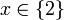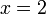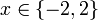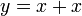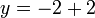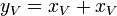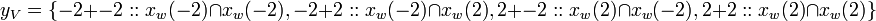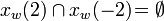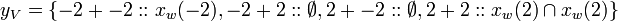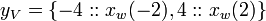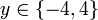User:Thepigdog/Value Set
Contents |
[edit] Summary
A Value Set is a type used in Constraint Logic Programming which is used to record a set of values allowed for a variables, attached to possible worlds. Value Sets allow us to reason about variables that may take multiple values.
A Value Set is a set of possible values for a variable. Constraint Logic Programming proceeds by "narrowing" this collection of values until only solution values are left. We need to know which "situation" each value is derived from. These situations are called possible worlds.
To describe Value Sets we first introduce possible worlds and then describe value sets in terms of possible worlds. Then we describe rules for working with Value Sets.
[edit] Possible Worlds
In general a Possible World may be thought of as an alternate possible reality that may eventuate under certain conditions.
Specifically in our case a Possible World is described by facts about the values of variables. The possible world is regarded as a set of outcomes and is represented in set builder notation like,
Note that we dont actually specify what the elements of the set are. The elements could be regarded as tuples of values of variables, but this is not necessary for our purposes.
In implementing a Constraint Logic Programming system Possible Worlds are not used to record boolean conditions. Possible Worlds are represented by their identity, and there hierarchical relationship.
However in proving theorems we will regard Possible Worlds as sets controlled by boolean conditions.
[edit] Possible World Set
A Possible World Set is a Partition of a Possible World P. It is a set of possible worlds S such that,
- if
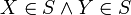 then
then 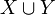 is empty.
is empty.
[edit] Value Set
A Value Set is a set of tagged values. Each value is "tagged" with a possible world that allows us to track the value against a possible world in a calculation. A tagged value is defined by the operator ::
The value of 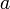 is
is 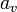 .
The possible world of
.
The possible world of 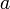 is
is 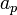
Value Sets are used to model the set of solutions to equations,
[edit] Extended Value
An extended value ev(x,xV) is a pair,
- x is a variable
- xV is a value set
The following functions are defined,
A set of values,
A set of worlds,
An extended value is valid if,
[edit] Definition A1
Description
- A variables value is in the set of values.
Definition
[edit] Definition A2
Description
- The possible worlds from a Value Set form a World Set.
Definition
[edit] Defintion A3
Description
- A World Set covers all possiblities.
Definition
[edit] Definition A4
Description
- The possible world for a value for a variable, must have that variable with that value.
Definition
[edit] Definition A5
Description
- Asserting a value set is equivalent to asserting the value.
Definition
This is the definition of what it means to type cast a value set to boolean. If a variable is of type boolean then its value set, type cast to boolean, is equal to the value.
[edit] Definition A6
Description
- The value set of a function call on a variable is the same as the value set of the function set applied to the value set of the variable.
Definition
for constant functions this reduces to,
[edit] Basic Theorems
[edit] Theorem T1
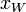 is a partition of
is a partition of 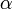 .
.
This follows from A3 and A4.
[edit] Theorem T2
There exists world sets 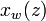 such that,
such that,
Proof:
Using this value for 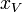 in A1 gives.
in A1 gives.
implies
[edit] Other stuff
The Possible Worlds can be given names 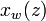 so,
so,
Using this definition (A1) and (A2) definition can also be written,
- (A1a)
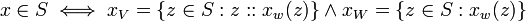
- (A1b)
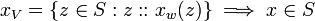
[edit] (B) Functions of a Value Set
The following theorem gives the function on a value set of a type using the function of the type.
- (B1)
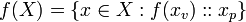
Note that for a tagged value x,
[edit] Function of multiple Parameters
If we allow Currying then we can extend the above definition to multiple parameters.
If currying is allowed,
The following theorem may then be used,
If F is a value set of functions on a value set of a values,
- (B2)
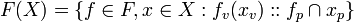
[edit] Function of two parameters
Then the definition for value sets of functions may be applied giving,
or,
- (B3)
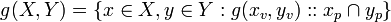
The result can be extended to more parameters.
[edit] (C) Assertions on Value Sets
The above rules allow us to transform a function of variable values into a function about value sets. A statement is a function that is asserted to return the true boolean value. A statement may be transformed into a function that returns a value set.
This is unusual because we dont normally assert a set to be true. But we can think of this polymorphically. A statement returning a value set may be treated differently from a statement returning a boolean.
In this case if V is a value set, the following law applies,
- (C1)
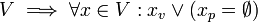
In words, if we assert a Value Set then for every tagged value in the set either the value is true or its possible world is empty. A value tagged with an empty possible world is an impossible value,
- (C2)
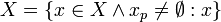
In other words you can remove all values tagged with the empty possible world from a value set.
[edit] Examples
[edit] Example 1
Clearly x = 2. But I want to show how this value is derived using value sets. Ultimately the application of these rules is automated into a logic programming system.
[edit] Step 1: Apply A
Using A1,
Using A5 and A6,
Note that the 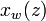 are possible worlds from a possible world set in
are possible worlds from a possible world set in 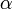 (the actual world).
(the actual world).
[edit] Step 2: Apply B
Using (B1) on 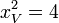 ,
,
which simplifies down to,
[edit] Step 3: Apply C
Using (C1),
gives 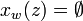 unless
unless 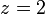 or
or 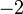 ,
,
Using (C2)
[edit] Step 4: Apply B again
Using (B1) on 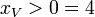 ,
,
[edit] Step 5: Apply C again
Using (C1),
gives 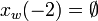 and so,
and so,
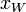 is a possible world set of
is a possible world set of 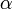 (the actual world). As all the possible worlds in the world set except
(the actual world). As all the possible worlds in the world set except 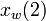 are empty we get,
are empty we get,
then from (A1),
or,
[edit] Example 2
This example shows how repeated use of a variables are handled. Naively,
But this possiblity is removed because the two values are from possible worlds whose intersection is empty.
[edit] Step 1: Apply A
Applying (A1a),
And using (A4a) and (A4b),
[edit] Step 2: Apply B
Using (B3),
but,
so,
or,
[edit] Step 3: Apply A
[edit] Conclusion
The steps shown in the examples are suited for automating into a algorithm that implements constraint logic programming. The rules are described as mathematics first to give the theory the widest applicability.