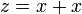User:Thepigdog/Logical Branching
Contents |
[edit] Purpose of Web Page
This page describes logical branching as an evaluation strategy for evaluating variables constrained by equations, and the principle of minimum branching as a strategy for solving problems.
Logic branching is similar to Logic Programming, and Constraint Logic Programming. A set of equations is organised in a particular so that they may be used to evaluate variables constrained by them.
Logic Branching aims to give a more structured theory for the evaluation of variables constrained by certain types of equation.
[edit] Summary
Instead of evaluating functions in a pre-chosen order the order of evaluation is controlled by a cost function. This allows an optimal evaluation order to be chosen.
A call to a function is used to evaluate the requested unknown value using the known values.
These two strategies give an efficient evaluation strategy, at the cost of of deferring the evaluation of functions.
To support this strategy variables must be allowed to support multiple values, associated with possible worlds.
[edit] Logic
Mathematical statements are functions that return a true value.
The process of solving mathematical equations allows them to be put in a form where the value of unknown variables may be read. However as we will see it is not necessary to solve equations for simple cases.
For example,
you can solve the equations as,
But for simple inversible functions it is not necessary to solve the whole equation. By adding a variable for each result of a function call the equation may be written,
these individual equations can be solved as,
So the solving of equations using inverses can be done at a local level,
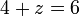 implies
implies 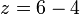
In general a function f
may be used to determine the unknown values from the known values.
[edit] Lazy Evaluation
Lazy evaluation proceeds by only attempting to evaluate a variable if its value is requested. In the above example if the value of x is requested we would proceed by looking at the equation,
This equation has two unknowns so in order to evaluate x we need the value for z. This leads us to request the value z from the equation.
We interpret this to mean that the + operator, called with 4 and z as parameters must return 6. This gives us the value 2 for z.
Now that z is known, we can use,
to give x = 1.
[edit] Tagged Branching
Some functions dont have nice inverse functions that return a single value. For example,
gives two possible values x = 2 or x = − 2.
Then both values must be considered. This may be written,
The method used in this case is tagged branching. We record two possible values for the variable x, eached tagged with a possible world. We represent that x = 2 in the possible world A and x = -2 in the possible world called B by,
Here [2::A, − 2::B] is called a tagged value set. It is a set of values, each identified by a possible world. The two possible worlds are named here A and B. The two worlds A and B form a possible world set. If we then add a condition,
then the value for x in possible world A satisfies the equation but value for x in possible world B does not. This leads to a contradiction in world B, destroying that possible world, leaving,
But now A + B together were all the possible worlds in a possible world set, so with B gone A reduces back to the actual world (which we call 0).
which we can write as,
[edit] Combination of possible worlds
When possible worlds combine there is a cartesian product of the results. For example,
then,
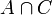 is a world created from the intersection of two possible worlds. The worlds
is a world created from the intersection of two possible worlds. The worlds 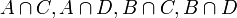 are children of the worlds from which they are combined. When either parent world is destroyed (by causing a contradiction) the child world is destroyed.
are children of the worlds from which they are combined. When either parent world is destroyed (by causing a contradiction) the child world is destroyed.
[edit] Minimizing the combinatorial explosion
The cardinality of the cartesian product of value sets may quickly grow to large numbers. Proceeding with calculations first that have less combinations will prove advantageous because each such calculation may add a constraint that destroys a possible world. We would like to perform calculations with less combinations first.
[edit] Delayed Evaluation
Usually when a function is called it is not necessary to construct a cartesian of product of value sets. Instead parameters may be passed through as value sets, delaying the evaluation. However when internal functions such as multiplication and division are encountered it is necessary to construct the cartesian product of value sets.
[edit] Cardinality of a calculation
A function call like,
has 4 variables r, x, y, z.
Take one variable as the value to be calculated. This will be the requested variable with the minimum branching.
The cardinality of the cartesian product of the other variables value sets is the Cardinality of a calculation.
[edit] Variables with a fixed number of values
A boolean variable v has two values true or false,
where K and L are possible worlds created for this variable. Any boolean may be expanded in this way.
Any variable with a fixed set of values may be handled in a similar manner.
[edit] The purpose of possible world tagging
If values were not tagged with possible worlds it would not be possible to know what world they came from.
- When the world showed an inconsistency it would not be possible to remove the value.
- We would not be able to detect when values are used from different possible worlds in the same world set.
For example if we have,
then,
does not mean that z may equal 2 + -2 = 0. This would be the case if we took the first x as 2 and the second x as -2.
This clearly wrong. The rule is that we cannot combine values from different possible worlds from the same possible world set.
[edit] Minimise size of value set
To minimize combinatorial explosion, calls to functions whose parameter evaluation cannot be delayed should be performed in order of the estimated number of entries in the resulting value set.
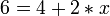

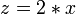
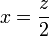
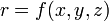
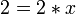
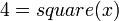
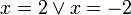
![x = [2::A, -2::B]\!](../../w/images/math/a/1/6/a1699cc1a146cbeb9030051012d3bbb2.png)
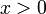
![x = [2::A]\!](../../w/images/math/2/a/4/2a4a08101241d101e0bf546d196a8c94.png)
![x = [2::0]\!](../../w/images/math/e/4/a/e4add1b0284801655548417f1cddd3b6.png)
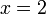
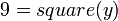
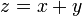
![y = [3::C, -3::D]\!](../../w/images/math/d/3/8/d38c5b3b04e8efced16e270dbc7a2957.png)
![z = [5::A\cap C, -1::A\cap D, 1::B\cap C, -5::B\cap D]](../../w/images/math/b/c/d/bcd7333a30ca0ca497ea321cd3ee9635.png)
![v = [true::K,\ false::L]](../../w/images/math/b/6/2/b62e0e19a984ad6ce41dbb2405fbb72f.png)