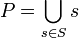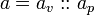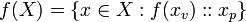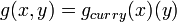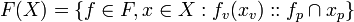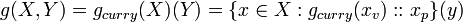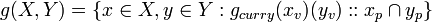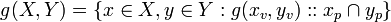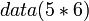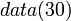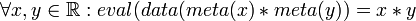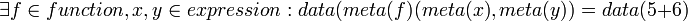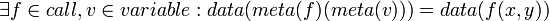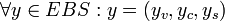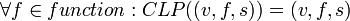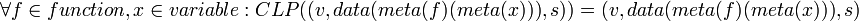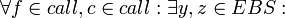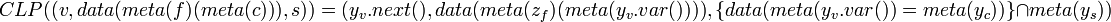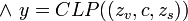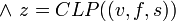User:Thepigdog/Constraint Logic Programming Theory
Contents |
[edit] Purpose of this Web Page
The purpose of this web page is to describe a formal theory of Constraint Logic Programming.
Constraint Logic Programming is an approach to evaluating the values of variables constrained by equations.
[edit] Summary
Variables have inital sets of values described by there type. Each equation or statement constrains or narrows the values that variables may hold. An equation or statement is an expression that evaluates to true.
The values that a variable may hold are held in value sets. Each value is tagged against a Possible World, which may be considered as an alternate possibility.
By arguing backwards from the final results sets of of values may be determined or narrowed.
The order of evaluation may be chosen so as to minimise the size of the value sets that are created. This approach gives an efficient method of evaluating the constrained variables.
[edit] Definitions
In this section I attempt to formally describe the general statements made above.
The ideas involved here are fairly simple. However generalising the description always makes it harder to understand.
[edit] Possible Worlds
A Possible World is a logically a set of bindings of variables to values. However we do not usually explicitly represent these bindings.
Possible worlds are sets and behave like sets,
The intersection of Possible Worlds M and N obeys the set laws,
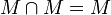
- If
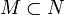 then
then 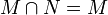
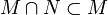
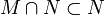
Each possible world is a sub-world (sub set) of the actual world which we refer to as α.
A possible world must have one and only value for each variable. If a contradiction is found then the possible world does not exist.
A possible world may have sub worlds grouped as Possible World Sets.
[edit] Possible World Set
A Possible World Set is a Partition of a Possible World P. It is a set of possible worlds S such that,
- if
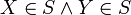 then
then 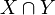 is empty.
is empty.
[edit] Value Set
A Value Set is a set of tagged values. A tagged value is defined by the operator ::
The value of 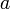 is
is 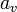 .
The possible world of
.
The possible world of 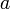 is
is 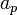
Value Sets arise naturally as the solutions of some kinds of equations,
- x2 = 4
also types with a finite set of values may be treated as value sets. Having obtained value sets we need rules for combining the results of value sets.
[edit] Functions of a Value Set
Suppose f is a function on a type T. We want to extend this definition to apply to value sets of type T also.
If we allow polymorphic functions polymorphic then we can also define,
- f is a function on a value set of type T,
The following definition defines the function on a value set of a type using the function of the type.
[edit] Function of multiple Parameters
If we allow Currying then we can extend the above definition to multiple parameters.
If currying is allowed,
The following defintion may then be used,
If F is a value set of functions on a value set of a values,
[edit] Function of two parameters
Then the definition for value sets of functions may be applied giving,
or,
The result can be extended to more parameters.
[edit] Meta Mathematics
We want to write a program that implements Constraint Logic Programming. Before we write such a program we would like to describe its behaviour in the language of mathematics. This is mathematics about mathematics, or Meta-Mathematics.
To do this we need to be able to treat the target mathematics as data to be described by the rules in the meta mathematics. But for clarity we would like this mathematical data to look like mathematics. We want the data describing the target mathematics to be represented syntactically like mathemematics.
[edit] Data
We add a special function data that takes a mathematical expression as a parameter. This construct means the data describing the mathematical expression. For example,
Is the data descibing the application of the operator * to the values 5 and 6. It is not the same as the value returned by the function. So it is distinct from,
"data" is a special function because is role is to change the meaning of text that appears for the parameter. The text within, although looking like mathematics, represents data structures describing the mathematics, not the results of the mathematical calculations.
[edit] Meta
We will be writing functions, in the meta mathematics that transform the data. In order to do this it helps to be able to use values from the meta mathematics within the data. This is achieved using the special function "meta".
For example we may want to describe the evaluation of x * y by an evaluation function,
[edit] Meta Types
In writing meta programs it helps to have some standard types;
- function - The name of a function,
- variable - A variable
- call - a call to a function.
- expression - any mathematical expression.
Note that although the use of infix operators and other syntactic devices is usefull to the human reader, to the computer it is just noise. So,
- 5 + 6 = + (5,6)
and more importantly,
binds
- f = data( + )
- x = data(5)
- y = data(6)
[edit] Currying
Currying of functions may be performed which means that,
- f(x,y) = fcurry(x)(y)
This means that,
binds,
- f = data(fcurry(x))
- v = data(y)
This is useful because it allows us to write meta expressions that breakdown functions of multiple parameters into functions or one parameter. Each parameter can then have rules applied to it.
[edit] Transformations of Mathematics
We wish to transform target mathematics,
- To apply functions value sets of a type instead of the type.
- To break up compound expressions into simple expressions linked by variables.
- To choose function or inverse functions to calculate the known from the unknown values.
[edit] Breaking up Compound Expressions
The Expression Breakdown Structure (EBS) is a triple,
- variable generator
- mathematical data describing an expression (the input expresion being processed).
- a set of simple mathematical equations.
The CLP function breaks up compound function calls into individual function calls linked by variables.