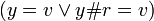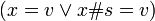User:Thepigdog/Church-Rosser Theorem
This theorem says that reduction may proceed in different orders, and still arrive at the same expression. The theorem allows us to think of Lambda Calculus expressions as representing a value.
The Church-Rosser Theorem states that if you start with an initial expression and perform two different series of reductions on it, to reach two different expressions, there is always a set of reduction for each expression that will reduce it to the same expression. This gives the basis for considering reductions as evaluating expressions. If lambda expressions reduced too different expressions in normal form then it would not be possible to consider the normal form as the value of the function.
However Deductive lambda calculus shows that Lambda Calculus is mathematical under certain conditions, and that under those conditions each expression represents a value. This makes the Church-Rosser Theorem less important, but it does not prove the theorem.
[edit] Church-Rosser Theorem
If L is a lambda expression, and M and N are both obtained from L by a series of beta or eta reductions then there exists a series of reductions for M and N that will reduce them to the same expression Z.
[edit] Etymology of the proof
The proof given below varies slightly from the proof given in [1] due to Tait and Martin-L¨of. That proof combines multiple reduction steps into a single step, and then considers the "Maximal one step reduction" as the point in the diamond. The theorem is then proved by combining the diamonds, to form a larger diamond like structure, the top of which is the original lambda expression, the edge points are the two expressions derived from it, and the bottom point is the Z which brings the values back together again.
This proof creates a definition of a beta reduction step based on the name of the variable in the lambda abstraction. This also allows multiple beta reduction steps to be considered as one step. With this definition, the reduction is commutative, but with some conditions. The conditions do not restrict the construction of the diamond structure as for the above proof.
This proof is given because I found the existing proof long and hard to follow. Also I found it disconcerting that the actual series of reductions to obtain Z was not constructed. Thirdly I like the fact that the reductions are commutative (under conditions), and I thing this gives a clearer intuitive insight into why the Church-Rosser Theorem is true.
[edit] Outline of the proof
Each beta reduction is a function that transforms a lambda expression into another lambda expression. If we have an initial expression L and M and N obtained from L by beta reductions then,
where
- m1,m2,...mr,n1,n2,...ns are beta reductions.
then,
and the Church-Rosser Theorem is proved if O = P.
If we could prove that the order of the application of beta reductions does not effect the result then we would have proved that O = P. So this would mean that if two reductions as x and y are composed then,
This result will be proved but with restrictions on when it is valid. However with the restrictions will not block the proof that O = P.
[edit] Beta and Eta Reduction Functions
The definitions of beta and eta reductions do not give us an explicit representation of a specific beta or eta reduction. The proof will proceed by creating functions that represent reductions. A beta reduction is defined as being applied to any lambda abstraction in the expression. But the function should be a beta reduction applied to a particular lambda abstraction. How is the sub-expression the beta or eta reduction is to be applied to identified?
If canonical renaming is applied then every lambda expression expression has it's own unique variable. Then the name of the variable can be used to identify the lambda expression to which to apply the reduction. Two functions will be defined,
- βf[x] performs a beta reduction βr on all lambda abstractions with the name x
- ηf[x] performs an eta reduction ηr on all lambda abstractions with the name x
But after a beta reduction a lambda abstraction may have been substituted a number of times. The βf and betaf functions are defined to reduce all lambda abstractions matching the name. A proof that this definition implies 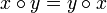 is given later, but there are conditions, and the definition needs to be refined further.
is given later, but there are conditions, and the definition needs to be refined further.
[edit] Valid reductions
A lambda abstraction without a parameter is a function. A beta reduction may substitute a lambda expression for a variable, giving it a parameter. This would mean that the βf applied before the beta reduction cannot be applied, because there is no parameter, but after the beta reduction the βf can be applied. This would break 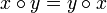 .
.
To avoid this situation we define valid application of a beta or eta reduction,
- For a βf[x] be validly applied, every lambda expression matching the name x must have a parameter.
[edit] A problem with names
A betaredexf is defined to perform all reductions on lambda abstractions matching the variable name. But this does not define a single beta reduction. For the first beta reduction a canonical renaming can be performed first. But for the second step a beta reduction may have created multiple copies of the lambda abstraction all with the same name.
We want to keep the names so that the betaredexf can be re-ordered, but change them so that they are distinct.
To achieve this add a name qualification scheme. An alpha renaming can change a name by adding a suffix after a period. So x is renamed to x#a.
Betaredexf is redefined to beta reduce all lambda abstractions matching the prefix.
A new kind of canonical renaming is defined that keeps the existing name but adds the unique name as a suffix. Then the betaredexf is the same before and after the canonical renaming.
[edit] Defintion of beta redex function
-
![\beta _{f} [x][(\lambda w.y)\ z] = \beta _{r} [(\lambda w.\beta _{f} [x][y])\ \beta _{f} [x][z]] \and (x = w \or x\#s = w)](../../w/images/math/5/4/d/54d75e46b205b91c08e0b692a2688755.png)
-
![\beta _{f} [x][\lambda w.y] = \lambda w.\beta _{f} [x][y] \and \neg (x = w \or x\#s = w)](../../w/images/math/e/a/f/eafd7888629687e05babc7b0d5fb7209.png)
-
![\beta _{f} [x][y \ z] = \beta _{f} [x][y]\ \beta _{f} [x][z]](../../w/images/math/7/9/6/7960986f43ab41cd5b3acecebefe672c.png)
- βf[x][v] = v
Note there is no case for ![(x = w \or x\#s = w) \and \beta _{f} [x][\lambda w.y]](../../w/images/math/4/9/b/49b792eb916f32d005bad02fc2f8e316.png) , with no application of the function to a parameter. If this condition occurs it is not a valid reduction.
, with no application of the function to a parameter. If this condition occurs it is not a valid reduction.
[edit] Defintion of eta redex function
-
![\eta _{f} [x][\lambda w.y\ w] = \eta _{f} [x][y] \and (x = w \or x\#s = w)](../../w/images/math/f/2/3/f23116bc164cf8d98f7045a40de90f0e.png)
-
![\eta _{f} [x][\lambda w.y\ z] = \lambda w.\eta _{f} [x][y]\ \eta _{f} [x][z] \and (w \ne z \or \neg (x = w \or x\#s = w))](../../w/images/math/1/5/3/15311edc5110465cc7fed131d0b5cb3b.png)
-
![\eta _{f} [x][y\ z] = \eta _{f} [x][y]\ \eta _{f} [x][z]](../../w/images/math/1/c/1/1c14d67fb1573c9b2a33b94549c5425a.png)
- ηf[x][v] = v
[edit] Proof that valid beta reduction functions commute
βf applied with βf.
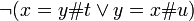
- X = βf[x]
- Y = βf[y]
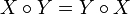
or
- X[Y[l]] = Y[X[l]]
Note that 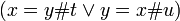 is a condition where commutativity does not hold.
is a condition where commutativity does not hold.
Proof by induction on all the cases of the lambda expression l. In each inductive case assume that the theorem holds for the parameters.
The proof is summarized in the following table with columns,
- Case name - The type of lambda expression, and any logical pre-conditions
- Lambda abstraction
- Application
- Variable
- Expression - The expression that needs to be shown true
- Simplified Expression - The expression re-arranged to show that it is true if the dependent cases, and inductive preconditios are true.
- Dependent case - Conditions that must be proven separately.
- Inductive preconditions - Conditions that are assumed true for the purpose of induction.
| Case name | Expression | Simplified | Dependent cases | Inductive pre-condition |
|---|---|---|---|---|
| Abs
|
X[Y[λv.m]] = Y[X[λv.m]] | λv.X[Y[m]] = λv.Y[X[m]] | none |
X[Y[m]] = Y[X[m]] |
| Abs (no parameter)
|
X[Y[λv.m]] = Y[X[λv.m]] | either X or Y is not valid βf | Invalid. |
X[Y[m]] = Y[X[m]] |
| Abs
|
![X[ Y[\lambda v.m\ n] ] = Y[ X[\lambda v.m\ n] ]](../../w/images/math/c/5/f/c5fbbfa4e58bfc41c1eb078b7347db4f.png)
|
Y[m][v: = Y[n]] = Y[m[v: = n]] |
Y[m][v: = Y[n]] = Y[m[v: = n]]
|
None |
| Abs
|
![X[ Y[\lambda v.m\ n] ] = Y[ X[\lambda v.m\ n] ]](../../w/images/math/c/5/f/c5fbbfa4e58bfc41c1eb078b7347db4f.png)
|
X[m[v: = n]] = Y[m[v: = n]] |
Not commutative if,
|
None |
| Abs
|
![X[ Y[\lambda v.m\ n] ] = Y[ X[\lambda v.m\ n] ]](../../w/images/math/c/5/f/c5fbbfa4e58bfc41c1eb078b7347db4f.png)
|
![X[ X[\lambda v.m\ n] ] = X[ X[\lambda v.m\ n] ]](../../w/images/math/c/0/b/c0bb573a714774901de76e362363ad5d.png)
|
None | None |
| Application | ![X[ Y[m\ n] ] = Y[ X[m\ n] ]](../../w/images/math/4/e/b/4ebff8b7c9bf2aa14121be631b20390e.png)
|
![X [ Y[m] ]\ X[ Y[n] ] = Y[ X [m] ]\ Y[ X[n] ]](../../w/images/math/6/6/a/66a8c2a5f2e099e6bfdee8c75252ea46.png)
|
none |
X[Y[m]] = Y[X[m]] X[Y[n]] = Y[X[n]] |
| Variable | X[Y[v]] = Y[X[v]] | v = v | none | none |
[edit] Proof of the substitution case
- Y = βf[y]
![Y[m][v := Y[n]] = Y[ m[v := n] ] \and \neg (y = v \or y = v\#r)](../../w/images/math/c/3/2/c32e32880db3a60ce039757992809484.png)
| Case name | Expression | Simplified | Dependent cases | Inductive pre-condition |
|---|---|---|---|---|
| Abstraction m | ![Y[\lambda y.b\ c][v := Y[n]] = Y[ (\lambda y.b\ c)[v := n] ]](../../w/images/math/6/0/6/606202156ca0f9c17301d0846c5a6263.png)
|
Y[b][y: = Y[c]][v: = Y[n]] = Y[b[v: = n]][y: = Y[c[v: = n]]]
|
[y: = Y[c]][v: = Y[n]] = [v: = Y[n]][y: = Y[c][v: = Y[n]]] |
Y[c][v: = Y[n]] = Y[c[v: = n]] Y[b][v: = Y[n]] = Y[b[v: = n]] |
| Abs not a = b | ![Y[\lambda a.b\ c][v := Y[n]] = Y[ (\lambda a.b\ c)[v := n] ]](../../w/images/math/7/9/9/79965f7faa3dbe98c9a027fdf2d23c70.png)
|
![(\lambda a.Y[b][v := Y[n]]\ Y[c][v := Y[n]]) = (\lambda a.Y[b[v := n]]\ Y[c[v := n])] ]](../../w/images/math/d/f/5/df59c0c0980bd62835dc714be671749f.png)
|
None |
Y[c][v: = Y[n]] = Y[c[v: = n]] Y[b][v: = Y[n]] = Y[b[v: = n]] |
| Application | ![Y[p\ q][v := Y[n]] = Y[ (p\ q)[v := n] ]](../../w/images/math/c/d/6/cd68449e9f4d90be78e3a0e42cb059a0.png)
|
![Y[p][v := Y[n]]\ Y[q][v := Y[n]] = Y[p[v := n]]\ Y[q[v := n]]](../../w/images/math/7/e/8/7e8eac8d268e6a914b9ee4c72848da3e.png)
|
None |
Y[p][v: = Y[n]] = Y[p[v: = n]] Y[q][v: = Y[n]] = Y[q[v: = n]] |
| Variable | Y[v][v: = Y[n]] = Y[v[v: = n]] | Y[n] = Y[n] | None | None |
| Variable not w = v | Y[w][v: = Y[n]] = Y[w[v: = n]] | w = w | None | None |
The dependent case,
- [y: = Y[c]][v: = Y[n]] = [v: = Y[n]][y: = Y[c][v: = Y[n]]]
can be written as,
- [y: = A][v: = B] = [v: = B][y: = A[v: = B]]
Proof omitted.
[edit] Proof that valid eta reduction functions commute
ηf applied with ηf.
- X = ηf[x]
- Y = ηf[y]
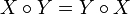
or
- X[Y[l]] = Y[X[l]]
Proof by induction on all the cases of the lambda expression l.
| Case name | Expression | Simplified | Dependent cases | Inductive precondition |
|---|---|---|---|---|
Abs 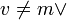
|
X[Y[λv.mn]] = Y[X[λv.mn]] | ![\lambda v.(X[Y[m]]\ (X[Y[m]]) = \lambda v.(Y[X[m]]\ (Y[X[m]])](../../w/images/math/7/5/1/751ab0181d923c820c2e962e0be988d9.png)
|
none |
X[Y[m]] = Y[X[m]] X[Y[n]] = Y[X[n]] |
| Abs
|
X[Y[λv.mv]] = Y[X[λv.mv]] | X[Y[m]] = Y[X[m]] | none |
X[Y[m]] = Y[X[m]] |
| Application | ![X[ Y[m\ n] ] = Y[ X[m\ n] ]](../../w/images/math/4/e/b/4ebff8b7c9bf2aa14121be631b20390e.png)
|
![X [ Y[m] ]\ X[ Y[n] ] = Y[ X [m] ]\ Y[ X[n] ]](../../w/images/math/6/6/a/66a8c2a5f2e099e6bfdee8c75252ea46.png)
|
none |
X[Y[m]] = Y[X[m]] X[Y[n]] = Y[X[n]] |
| Variable | X[Y[v]] = Y[X[v]] | v = v | none | none |
[edit] Proof that valid beta reduction functions commute with eta
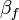 applied with
applied with 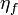 .
.
or
Proof by induction on all the cases of the lambda expression l.
| Case name | Expression | Simplified | Dependent cases | Inductive precondition |
|---|---|---|---|---|
| Abs
|
![X[ Y[\lambda v.m n] ] = Y[ X[\lambda v.m n] ] \!](../../w/images/math/d/4/1/d4173bdae93693a147fce9892cb3d11a.png)
|
![\lambda v.X[Y[m]]\ X[Y[n]] = \lambda v.Y[X[m]]\ Y[X[n]] \!](../../w/images/math/5/a/9/5a9d58fee2646739feb8c9adc147fa18.png)
|
none |
|
| Abs
|
![X[ Y[\lambda v.m v] ] = Y[ X[\lambda v.m v] ] \!](../../w/images/math/a/9/9/a99a9a066801998e90d42ecf0bb93458.png)
|
![X[ Y[m] ] = Y[ X[m] ] \!](../../w/images/math/2/4/a/24abe046c41e051f093157dcd0515476.png)
|
none |
|
| Abs
|
![X[ Y[(\lambda v.m) n] ] = Y[ X[(\lambda v.m) n] ] \!](../../w/images/math/1/b/3/1b33986c5c9a530252ec2828f87eba79.png)
|
![X[Y[m]][v := X[Y[n]]] = Y[X[m][v := X[n]] ] \!](../../w/images/math/7/e/d/7ed3ae1f24dafb48f81c0f3f4ef24e79.png)
|
![X[Y[m]][v := X[Y[n]]] = Y[X[m][v := X[n]] ] \!](../../w/images/math/7/e/d/7ed3ae1f24dafb48f81c0f3f4ef24e79.png)
|
None |
| Abs
|
![X[ Y[(\lambda v.m\ v) n] ] = Y[ X[(\lambda v.m\ v) n] ] \!](../../w/images/math/9/e/5/9e5e50f5c8d8840a71b1f76f6867f154.png)
|
![X[Y[m]]\ X[Y[n]] = Y[X[m]]\ Y[X[n]] \!](../../w/images/math/3/7/d/37d9c2a77898a66f9525b34c9f66deeb.png)
|
None |
|
Abs 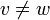
|
![X[ Y[(\lambda v.m\ w) n] ] = Y[ X[(\lambda v.m\ w) n] ] \!](../../w/images/math/2/d/f/2df312727f64dd468a273ad881b93f2d.png)
|
![X[Y[m]\ Y[w]][v := X[Y[n]]] = Y[ (X[m]\ X[w])[v := X[n]] ] \!](../../w/images/math/9/c/f/9cfe4f7e755af0b0a282953eeeeff759.png)
|
![X[Y[m]\ Y[w]][v := X[Y[n]]] = Y[ (X[m]\ X[w])[v := X[n]] ]](../../w/images/math/1/0/9/1097b4db933a28fc5d3f6290774b4730.png)
|
None |
| Application | ![X[ Y[m\ n] ] = Y[ X[m\ n] ] \!](../../w/images/math/6/c/9/6c9ca2f105571e4e323d10b6c7d406e2.png)
|
![X [ Y[m] ]\ X[ Y[n] ] = Y[ X [m] ]\ Y[ X[n] ] \!](../../w/images/math/3/7/d/37d9c2a77898a66f9525b34c9f66deeb.png)
|
none |
|
| Variable | ![X[ Y[v] ] = Y[ X[v] ] \!](../../w/images/math/c/e/5/ce5ffc806c2c8124688b1696f346e3b3.png)
|

|
none | none |
[edit] Links
[edit] References
- ↑ Lecture Notes on the Lambda Calculus. Peter Selinger
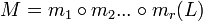
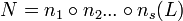
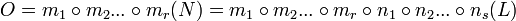
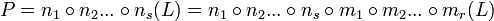
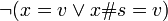
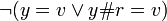
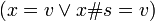
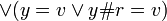
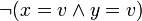
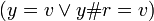
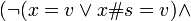
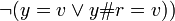
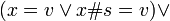
![X = \beta _{f} [x] \!](../../w/images/math/6/6/9/669623cac518f1943a2cc6b04ad786ca.png)
![Y = \eta _{f} [y] \!](../../w/images/math/1/1/0/110c1ce81b7172cd8cf5b00cb0829c88.png)
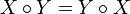
![X[ Y[ l ]] = Y[ X[ l ]] \!](../../w/images/math/a/e/6/ae6088b131825e67e529a85ad9dd91fc.png)
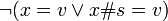
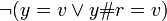
![X[ Y[n] ] = Y[ X[n] ] \!](../../w/images/math/a/b/b/abb9fabd54bcf41a67994487496d303d.png)