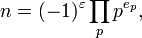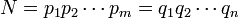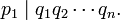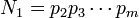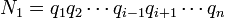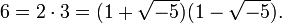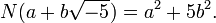Unique factorization/advanced
In mathematics, the unique factorization theorem, also known as the fundamental theorem of arithmetic states that every nonzero integer can be written in a unique way as a product of a unit (i.e., 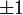 ) and prime numbers. Unique factorization is the foundation for most of the structure of whole numbers as described by elementary number theory. The formulation of many results (for instance, the Chinese remainder theorem) would either be nonsensical, or at least more complicated, if unique factorization did not hold.
) and prime numbers. Unique factorization is the foundation for most of the structure of whole numbers as described by elementary number theory. The formulation of many results (for instance, the Chinese remainder theorem) would either be nonsensical, or at least more complicated, if unique factorization did not hold.
Contents |
[edit] Precise formulation
The theorem has two parts: first, that a factorization exsits, and second, that it is unique. This description leads to a couple of troublesome questions. If we allow rearrangement of the factors, as in 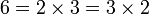 , the theorem is false. Also, what are the prime factorizations of 1 and -1?
, the theorem is false. Also, what are the prime factorizations of 1 and -1?
We can give a more precise version as follows. The first part of the theorem states that every nonzero integer n has a prime factorization. We can therefore write
this being an infinite product over the set of prime numbers. As n can have only finitely many prime factors, all but finitely many of the exponents ep are 0, so the product makes sense. Also, we can restrict  to be either 0 or 1 when n is positive or negative respectively, and all of the exponents ep must be nonnegative integers. With these conventions, the fundamental theorem can now be precisely expressed as saying that for any nonzero integer n, a factorization as above exists, and the list of integers
to be either 0 or 1 when n is positive or negative respectively, and all of the exponents ep must be nonnegative integers. With these conventions, the fundamental theorem can now be precisely expressed as saying that for any nonzero integer n, a factorization as above exists, and the list of integers 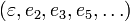 is uniquely determined by n.
is uniquely determined by n.
For a nonnegative integer n and a prime number p, the exponent ep in the factorization is called the order of n at p, written ordp(n). Consideration of these orders leads directly to the useful theory of valuations.
[edit] Proof
The proof of both the existence and uniqueness statements of the fundamental theorem requires the technique known as mathematical induction. The statement and proof can be easily generalized to principal ideal domains.
[edit] Existence
To see that every integer > 1 can be factored as the product of prime numbers, we begin the strong induction proof by observing that the first such integer, 2, is a product of primes (note: a single prime must itself be considered to be such a "product", or else the theorem would be false). We now fix an integer N and make the induction hypothesis by assuming that every integer between 2 and N-1 inclusive is already known to factor into the product of prime numbers. Upon considering a possible factorization of N, there are two cases: N is either prime or composite. If N is prime, then N by itself is a factorization into primes. Otherwise, N is composite. In other words, there exist integers m, n>1 such that N = mn. Thus, m = N / n, so 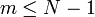 since n > 1. Similarly,
since n > 1. Similarly, 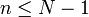 since m > 1. Thus, both of the integers m and n fall into the range of integers covered by the induction hypothesis, so they can both be written as products of prime numbers. But then N = mn can also be written as the product of prime numbers. By the principle of strong induction, it follows that every integer > 1 can be written as the product of prime numbers.
since m > 1. Thus, both of the integers m and n fall into the range of integers covered by the induction hypothesis, so they can both be written as products of prime numbers. But then N = mn can also be written as the product of prime numbers. By the principle of strong induction, it follows that every integer > 1 can be written as the product of prime numbers.
[edit] Uniqueness
Every integer N > 1 can be written in a unique way as a product of prime factors, up to reordering. To see why this is true, assume that N can be written as a product of prime factors in two ways
We may now use a technique known as mathematical induction to show that the two prime decompositions are really the same.
Consider the prime factor p1. We know that
Using the second definition of prime numbers, it follows that p1 divides one of the q-factors, say qi. Using the first definition, p1 is in fact equal to qi
Now, if we set N1 = N / p1, we may write
and
In other words, N1 is the product of all the q's except qi.
Continuing in this way, we obtain a sequence of numbers 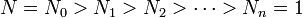 where each Nα is obtained by dividing Nα − 1 by a prime factor. In particular, we see that m = n and that there is some permutation ("rearrangement") σ of the indices
where each Nα is obtained by dividing Nα − 1 by a prime factor. In particular, we see that m = n and that there is some permutation ("rearrangement") σ of the indices 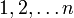 such that pi = qσ(i). Said differently, the two factorizations of N must be the same up to a possible rearrangement of terms.
such that pi = qσ(i). Said differently, the two factorizations of N must be the same up to a possible rearrangement of terms.
[edit] A number system where unique factorization fails
There are other systems of numbers that have striking similarities with the integers. One example is the Gaussian integers, ![\mathbb{Z} [\sqrt{-1}]](../../w/images/math/2/f/8/2f8c459be043bd27941aca415f800249.png) . A Gaussian integer is built up from the usual (or rational) integers and the extra number i, a square root of -1, through a finite number of additions, subtractions, and multiplications. We may think of the Gaussian integers as the smallest system of numbers that you can obtain if you want to throw i in with the rational integers. After simplification, a Gaussian integer can always be written in the form a + bi where a and b are rational integers. There is the natural notion of a prime Gaussian integer, where such Gaussian primes cannot be factored further in a certain sense. Also, there is a unique factorization theorem for the Gaussian integers, stating that each Gaussian integer can be factored as a product of Gaussian primes in an essentially unique way.
. A Gaussian integer is built up from the usual (or rational) integers and the extra number i, a square root of -1, through a finite number of additions, subtractions, and multiplications. We may think of the Gaussian integers as the smallest system of numbers that you can obtain if you want to throw i in with the rational integers. After simplification, a Gaussian integer can always be written in the form a + bi where a and b are rational integers. There is the natural notion of a prime Gaussian integer, where such Gaussian primes cannot be factored further in a certain sense. Also, there is a unique factorization theorem for the Gaussian integers, stating that each Gaussian integer can be factored as a product of Gaussian primes in an essentially unique way.
Surprisingly, there are other similar number systems where unique factorization does not hold. The classic example is ![\mathbb{Z} [ \sqrt{-5} ]](../../w/images/math/7/b/2/7b229623534053a04b838860278c1568.png) . A number in this system can always be written as
. A number in this system can always be written as 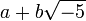 for some rational integers a and b. Once again, there are numbers in this system that can be considered to be 'atomic', in that they do not factor in any nontrivial way. In this context, such numbers are called irreducible, not prime, because in examples where unique factorization does not hold, the word 'prime' is reserved for a different use. A unique factorization theorem would state that every number in
for some rational integers a and b. Once again, there are numbers in this system that can be considered to be 'atomic', in that they do not factor in any nontrivial way. In this context, such numbers are called irreducible, not prime, because in examples where unique factorization does not hold, the word 'prime' is reserved for a different use. A unique factorization theorem would state that every number in ![\mathbb{Z} [\sqrt{-5} ]](../../w/images/math/7/b/2/7b229623534053a04b838860278c1568.png) can be factored as a product of irreducible numbers in an essentially unique way. The word "essentially" here means that the factorization is unique up to reordering the factors and multiplying by numbers dividing 1. It can be shown that the only numbers dividing 1 in this system are -1 and 1.
can be factored as a product of irreducible numbers in an essentially unique way. The word "essentially" here means that the factorization is unique up to reordering the factors and multiplying by numbers dividing 1. It can be shown that the only numbers dividing 1 in this system are -1 and 1.
Consider the following factorizations of 6 in ![\mathbb{Z} [\sqrt{-5}]](../../w/images/math/7/b/2/7b229623534053a04b838860278c1568.png) :
:
It turns out that 2, 3, and the numbers 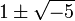 are each irreducible. As 1 and -1 are the only numbers dividing 1 in this system, these are two essentially different factorizations of 6 into irreducible numbers.
are each irreducible. As 1 and -1 are the only numbers dividing 1 in this system, these are two essentially different factorizations of 6 into irreducible numbers.
To see that the above numbers are irreducible, we need a tool, the field norm, which is the function from ![\mathbb{Z} [\sqrt{-5}]](../../w/images/math/7/b/2/7b229623534053a04b838860278c1568.png) to the integers given by
to the integers given by
Give properties, proof of UF here
[edit] Number systems with unique factorization
As mentioned above, unique factorization holds in ![\mathbb{Z} [\sqrt{-1}]](../../w/images/math/2/f/8/2f8c459be043bd27941aca415f800249.png) , but in
, but in ![\mathbb{Z} [\sqrt{-5}]](../../w/images/math/7/b/2/7b229623534053a04b838860278c1568.png) , numbers do not have unique factorizations into irreducible factors. It was the search for a remedy for this that led, first to the invention of ideal numbers by Kummer, and later to the development of ideals and ring theory by Dedekind. Eventually, unique factorization in this setting was salvaged by proving that the principal ideal generated by a number (and actually every ideal) has a unique factorization into prime ideals. For more on this, read about Dedekind domains.
, numbers do not have unique factorizations into irreducible factors. It was the search for a remedy for this that led, first to the invention of ideal numbers by Kummer, and later to the development of ideals and ring theory by Dedekind. Eventually, unique factorization in this setting was salvaged by proving that the principal ideal generated by a number (and actually every ideal) has a unique factorization into prime ideals. For more on this, read about Dedekind domains.
A ring is a mathematical structure similar to the integers, of which the integers, ![\mathbb{Z} [\sqrt{-1}]](../../w/images/math/2/f/8/2f8c459be043bd27941aca415f800249.png) , and
, and ![\mathbb{Z} [\sqrt{-5}]](../../w/images/math/7/b/2/7b229623534053a04b838860278c1568.png) are all examples. Rings are the appropriate mathematical setting in which to consider the concepts of irreducible factors and unique factorization. Those rings in which unique factorization holds are called unique factorization domains.
are all examples. Rings are the appropriate mathematical setting in which to consider the concepts of irreducible factors and unique factorization. Those rings in which unique factorization holds are called unique factorization domains.
| |
Some content on this page may previously have appeared on Citizendium. |