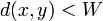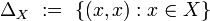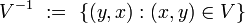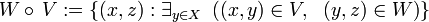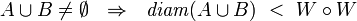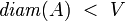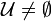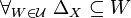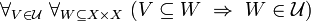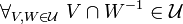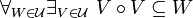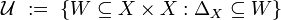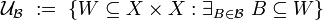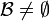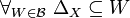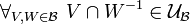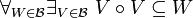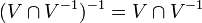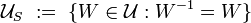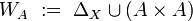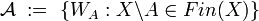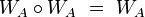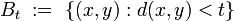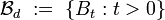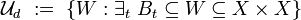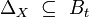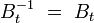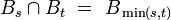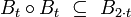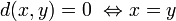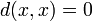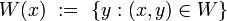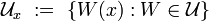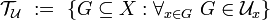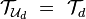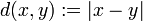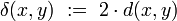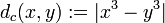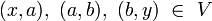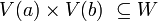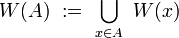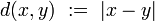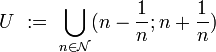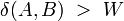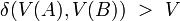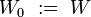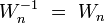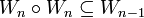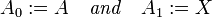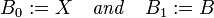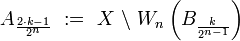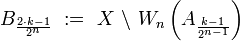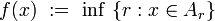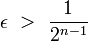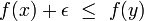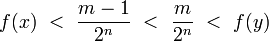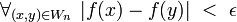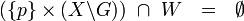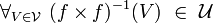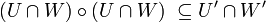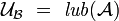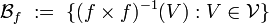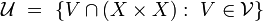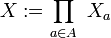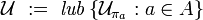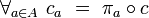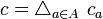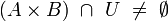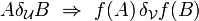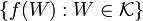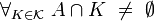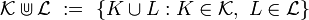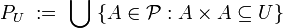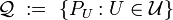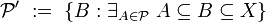Uniform space
In mathematics, and more specifically in topology, the notions of a uniform structure and a uniform space generalize the notions of a metric (distance function) and a metric space respectively. As a human activity, the theory of uniform spaces is a chapter of general topology. From the formal point of view, the notion of a uniform space is a sibling of the notion of a topological space. While uniform spaces are significant for mathematical analysis, the notion seems less fundamental than that of a topological space. The notion of uniformity is auxiliary rather than an object to be studied for its own sake (specialists on uniform spaces may disagree though).
For two points of a metric space, their distance is given, and it is a measure of how close each of the given two points is to another. The notion of uniformity catches the idea of two points being near one another in a more general way, without assigning a numerical value to their distance. Instead, given a subset 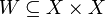 , we may say that two points
, we may say that two points 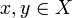 are W-near one to another, when
are W-near one to another, when 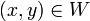 ; certain such sets
; certain such sets 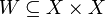 are called entourages (see below), and then the mathematician Roman Sikorski would write suggestively:
are called entourages (see below), and then the mathematician Roman Sikorski would write suggestively:
meaning that this whole mathematical phrase stands for: 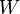 is an entourage, and
is an entourage, and 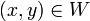 . Thus we see that in the general case of uniform spaces, the distance between two points is (not measured but) estimated by the entourages to which the ordered pair of the given two points belongs.
. Thus we see that in the general case of uniform spaces, the distance between two points is (not measured but) estimated by the entourages to which the ordered pair of the given two points belongs.
Contents |
[edit] Historical remarks
The ideas of uniformity, in the context of finite dimensional real linear spaces (Euclidean spaces), appeared already in the work of the pioneers of the precision in mathematical analysis (A.-L. Cauchy, E. Heine). Next, George Cantor constructed the real line by metrically completing the field of rational numbers, while Frechet introduced metric spaces. Then Felix Hausdorff extended the Cantor's completion construction onto arbitrary metric spaces. General uniform spaces were introduced by Andre Weil in a 1937 publication.
The ideas of uniformity may be expressed equivalently in terms of coverings. The basic idea of an abstract triangle inequality in terms of coverings has appeared already in the proof of the metrization Aleksandrov-Urysohn theorem (1923).
A different but equivalent approach was introduced by V.A.Efremovich, and developed by Y.M.Smirnov. Efremovich axiomatized the notion of two sets approaching one another (infinitely closely, possibly overlapping). In terms of entourages, two sets approach one another if for every entourage 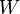 there is an ordered pair of points
there is an ordered pair of points 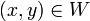 , one from each of the given two sets, i.e. for which the Sikorski's inequality holds:
, one from each of the given two sets, i.e. for which the Sikorski's inequality holds:
According to P.S.Aleksandrov, this kind of approach to uniformity, in the language of nearness, goes back to Riesz (perhaps F.Riesz).
[edit] Topological prerequisites
This article assumes that the reader is familiar with certain elementary, basic notions of topology, namely:
- topology (as a family of open sets), topological space;
- neighborhoods (of points and sets), bases of neighborhoods;
- separation axioms:
-
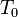 (Kolmogorov axiom);
(Kolmogorov axiom);
-
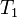
-
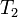 (Hausdorff axiom);
(Hausdorff axiom);
- regularity axiom and
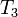
- complete regularity (Tichonov axiom) and
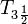 ;
;
- normal spaces and
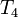 ;
;
-
- continuous functions (maps, mappings);
- compact spaces (and compact Hausdorff spaces, i.e. compact
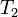 -spaces);
-spaces);
- metrics and pseudo-metrics, metric and pseudo-metric spaces, topology induced by a metric or pseudo-metric.
[edit] Definition
[edit] Auxiliary set-theoretical notation, notions and properties
Given a set  , and
, and 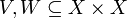 , let's use the notation:
, let's use the notation:
and
and
Theorem
-
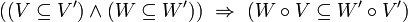
-
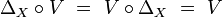
-
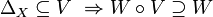
-
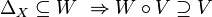
-
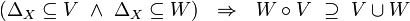
- if
 and
and  are
are  -sets (see the definition below), where
-sets (see the definition below), where 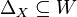 , and if
, and if 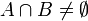 , then
, then 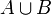 is a
is a 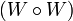 -set; or in the Sikorski's notation:
-set; or in the Sikorski's notation:
-
- for every
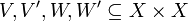 , and
, and 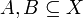 .
.
Definition A subset 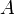 of
of 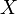 is called a
is called a 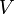 -set if
-set if 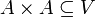 , in which case we may also use Sikorski's notation:
, in which case we may also use Sikorski's notation:
- Let
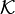 be a family of sets such that the union of any two of them is a
be a family of sets such that the union of any two of them is a 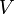 -set (where
-set (where 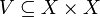 ). Then the union
). Then the union 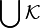 is a
is a 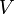 -set.
-set.
[edit] Uniform space (definition)
An ordered pair 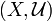 , consisting of a set
, consisting of a set  and a family
and a family 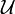 of subsets of
of subsets of 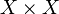 , is called a uniform space, and
, is called a uniform space, and 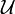 is called a uniform structure in
is called a uniform structure in  , if the following five properties (axioms) hold:
, if the following five properties (axioms) hold:
Members of 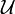 are called entourages.
are called entourages.
Instead of the somewhat long term uniform structure we may also use short term uniformity—it means exactly the same.
Example: 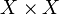 is an entourage of every uniform structure in
is an entourage of every uniform structure in  .
.
[edit] Two extreme examples
The single element family 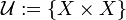 is a uniform structure in
is a uniform structure in  ; it is called the weakest uniform structure (in
; it is called the weakest uniform structure (in  ).
).
Family
is a uniform structure in  too; it is called the strongest uniform structure or the discrete uniform structure in
too; it is called the strongest uniform structure or the discrete uniform structure in  ; it contains every other uniform structure in
; it contains every other uniform structure in  .
.
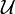 is the strongest uniform structure in
is the strongest uniform structure in  if and only if
if and only if 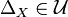 .
.
[edit] Uniform base
A family 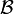 is called to be a base of a uniform structure
is called to be a base of a uniform structure 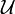 in
in  if
if 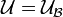 , where:
, where:
Remark Uniform bases are also called fundamental systems of neighborhoods of the uniform structure (by Bourbaki).
Instead of starting with a uniform structure, we may begin with a family 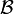 . If family
. If family 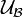 is a uniform structure in
is a uniform structure in  , then we simply say that
, then we simply say that 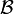 is a uniform base (without mentioning explicitly any uniform structure).
is a uniform base (without mentioning explicitly any uniform structure).
Theorem A family 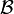 of subsets of
of subsets of 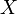 is a uniform base if and only if the following properties hold:
is a uniform base if and only if the following properties hold:
Remark Property 3 above features 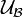 (it's not a typo!)--it's simpler this way.
(it's not a typo!)--it's simpler this way.
[edit] The symmetric base
Let 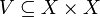 . We say that
. We say that 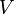 is symmetric if
is symmetric if 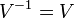 .
.
Let 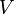 be as above, and let
be as above, and let 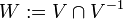 . Then
. Then 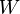 is symmetric, i.e.
is symmetric, i.e.
Now let 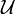 be a uniform structure in
be a uniform structure in  . Then
. Then
is a base of the uniform structure 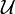 ; it is called the symmetric base of
; it is called the symmetric base of 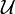 . Thus every uniform structure admits a symmetric base.
. Thus every uniform structure admits a symmetric base.
[edit] Example
Notation: 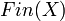 is the family of all finite subsets of
is the family of all finite subsets of  .
.
Let 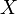 be an infinite set. Let
be an infinite set. Let
for every 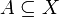 , and
, and
Each member of 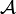 is symmetric. Let's show that
is symmetric. Let's show that 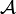 is a uniform base:
is a uniform base:
- Indeed, axioms 1-3 of uniform base obviously hold. Also:
- hence axiom 4 holds too. Thus
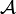 is a uniform base.
is a uniform base.
The generated uniform structure 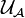 is different both from the weakest and from the strongest uniform structure in
is different both from the weakest and from the strongest uniform structure in  , (because
, (because 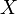 is infinite).
is infinite).
[edit] Metric spaces
Let 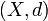 be a metric space. Let
be a metric space. Let
for every real 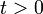 . Define now
. Define now
and finally:
Then 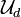 is a uniform structure in
is a uniform structure in  ; it is called the uniform structure induced by metric
; it is called the uniform structure induced by metric 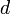 (in
(in  ).
).
Family 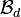 is a base of the structure
is a base of the structure 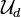 (see above). Observe that:
(see above). Observe that:
for arbitrary real numbers 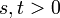 . This is why
. This is why 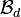 is a uniform base, and
is a uniform base, and 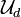 is a uniform structure (see the axioms of the uniform structure above).
is a uniform structure (see the axioms of the uniform structure above).
- Remark (!) Everything said in this text fragment is true more generally for arbitrary pseudo-metric space
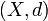 ; instead of the standard metric axiom:
; instead of the standard metric axiom:
- a pseudo-metric space is assumed to satisfy only a weaker axiom:
- (for arbitrary
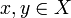 ).
).
[edit] The induced topology
First another piece of auxiliary notation--given a set  , and
, and 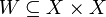 , let
, let
Let 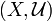 be a uniform space. Then families of sets
be a uniform space. Then families of sets
where 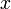 runs over
runs over  , form a system of neighborhoods in
, form a system of neighborhoods in  , defining a topology. The topology itself is defined as:
, defining a topology. The topology itself is defined as:
- The topology induced by the weakest uniform structure is the weakest topology. Furthermore, the weakest uniform structure is the only one which induces the weakest topology (in a given set).
- The topology induced by the strongest (discrete) uniform structure is the strongest (discrete) topology. Furthermore, the strongest uniform structure is the only one which induces the discrete topology in the given set if and only if that set is finite. Indeed, for any infinite set also the uniform structure
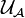 (see Example above) induces the discrete topology. Thus different uniform structures (defined in the same set) can induce the same topology.
(see Example above) induces the discrete topology. Thus different uniform structures (defined in the same set) can induce the same topology.
- The topology
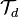 induced by a metrics
induced by a metrics 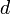 is the same as the topology induced by the uniform structure induced by that metrics:
is the same as the topology induced by the uniform structure induced by that metrics:
- Convention From now on, unless stated explicitly to the contrary, the topology considered in a uniform space is always the topology induced by the uniform structure of the given space. In particular, in the case of the uniform spaces the general topological operations on sets, like interior
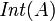 and closure
and closure 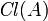 , are taken with respect to the topology induced by the uniform structure of the respective uniform space.
, are taken with respect to the topology induced by the uniform structure of the respective uniform space.
Example Consider three metric functions in the real line 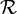 :
:
All these three metric functions induce the same, standard topology in 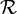 . Furthermore, functions
. Furthermore, functions 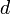 and
and 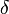 induce the same uniform structure in
induce the same uniform structure in 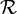 . Thus different metric functions can induce the same uniform structure. On the other hand, the uniform structures induced by
. Thus different metric functions can induce the same uniform structure. On the other hand, the uniform structures induced by 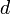 and
and 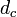 are different, which shows that different uniform structures, even when they are induced by metric functions, can induce the same topology.
are different, which shows that different uniform structures, even when they are induced by metric functions, can induce the same topology.
Theorem Let 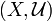 be a uniform space. The family of all entourages
be a uniform space. The family of all entourages 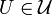 which are open in
which are open in 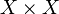 is a base of structure
is a base of structure 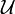
Remark An equivalent formulation of the above theorem is:
- the interior of every entourage is an entourage.
Proof (of the theorem). Let 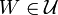 be an arbitrary entourage. Let
be an arbitrary entourage. Let 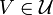 be a symmetric entourage such that
be a symmetric entourage such that 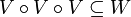 . It is enough to prove that entourage
. It is enough to prove that entourage 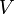 is contained in the topological interior of
is contained in the topological interior of 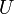 . Let's do it. Let
. Let's do it. Let 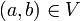 . Let
. Let 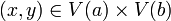 . Then, since
. Then, since 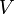 is symmetric, we have:
is symmetric, we have:
hence 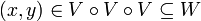 . This proves that
. This proves that
Thus every point 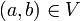 belongs to the topological interior of
belongs to the topological interior of 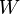 , i.e. the entire
, i.e. the entire 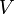 is contained in the interior of
is contained in the interior of 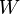 .
.
End of proof.
[edit] Separation properties
Notation:
for every entourage 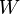 and
and 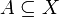 (see above the definition of
(see above the definition of 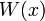 ). Thus
). Thus 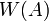 is a neighborhood of
is a neighborhood of 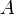 .
.
Warning 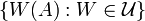 does not have to be a base of neighborhoods of
does not have to be a base of neighborhoods of 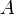 , as shown by the following example (consult the section about metric spaces, above):
, as shown by the following example (consult the section about metric spaces, above):
Example Let 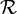 be the space of real numbers with its customary Euclidean distance (metric)
be the space of real numbers with its customary Euclidean distance (metric)
and the uniformity induced by this metric (see above)—this uniformity is called Euclidean. Let 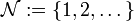 be the set of natural numbers. Then the union of open intervals:
be the set of natural numbers. Then the union of open intervals:
is an open neighborhood of 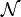 in
in 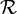 , but there does not exist any
, but there does not exist any 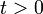 such that
such that 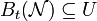 (see above). It follows that
(see above). It follows that 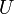 does not contain any set
does not contain any set 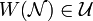 , where
, where 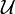 is the Euclidean uniformity in
is the Euclidean uniformity in 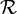 .
.
Definition Let 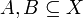 , and
, and 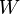 be an entourage. We say that
be an entourage. We say that 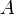 and
and 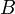 are
are 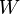 -apart, if
-apart, if
in which case we write
in the spirit of Sikorski's notation (it is an idiom, don't try to parse it).
- Let
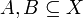 be
be 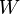 -apart. Let
-apart. Let 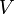 be another entourage, and let it be symmetric (meaning
be another entourage, and let it be symmetric (meaning 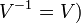 and such that
and such that 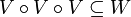 . Then
. Then 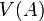 and
and 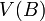 are
are 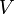 -apart:
-apart:
We see that two sets which are apart (for an entourage) admit neighborhoods which are apart too. Now we may mimic Paul Urysohn by stating a uniform variant of his topological lemma:
- Uniform Urysohn Lemma Let
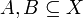 be apart. Then there exists a uniformly continuous function
be apart. Then there exists a uniformly continuous function ![\ f : X \rightarrow [0;1]](../w/images/math/0/f/9/0f9c03bc23bc310dd7ad44fd0bbc5274.png) such that
such that 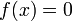 for every
for every 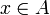 , and
, and 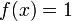 for every
for every 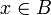 .
.
It is possible to adopt the main idea of the Urysohn's original proof of his lemma to this new uniform situation by iterating the statement just above the Uniform Urysohn Lemma.
- Proof (of the Uniform Urysohn Lemma)
- Let
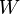 be an entourage. Let
be an entourage. Let 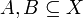 be
be 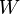 -apart. Let
-apart. Let 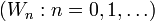 be a sequence of entourages such that
be a sequence of entourages such that
- for every
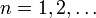 . Next, let
. Next, let 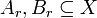 for every
for every 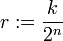 , where
, where 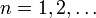 and
and 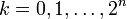 , be defined, inductively on
, be defined, inductively on 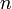 , as follows:
, as follows:
- for every
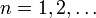 and
and 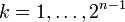 . We see that
. We see that
-
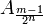 and
and 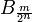 are
are 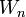 -apart for every
-apart for every 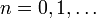 and
and 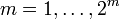 ;
;
-
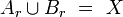 for every
for every  ;
;
- the assignment
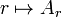 is increasing, while
is increasing, while 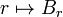 is decreasing.
is decreasing.
-
- The required uniform function can be defined as follows:
- for every
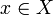 . Obviously,
. Obviously, 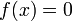 for every
for every 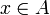 , and
, and 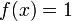 for every
for every 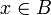 . Furthermore, let
. Furthermore, let 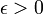 . Then
. Then
- for certain positive integer
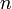 . Let
. Let 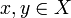 be such that
be such that
- Then there exists
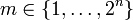 such that
such that
- Thus
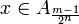 , while
, while 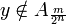 , hence
, hence 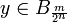 . Thus points
. Thus points 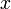 and
and 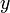 are
are 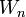 -apart.
-apart.
- We have proved that for every
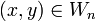 the images are less then
the images are less then  -apart:
-apart:
- End of proof.
Now let's consider a special case of one of the two sets being a 1-point set.
- Let
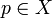 , and let
, and let 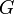 be a neighborhood of
be a neighborhood of 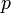 (with respect to the uniform topology, i.e. with respect to the topology induced by the uniform structure). Then
(with respect to the uniform topology, i.e. with respect to the topology induced by the uniform structure). Then 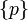 and
and 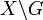 are apart.
are apart.
Indeed, there exists an entourage 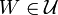 such that
such that 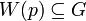 , which means that
, which means that
i.e. 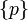 and
and 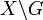 are
are 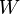 -apart.
-apart.
Thus we may apply the Uniform Urysohn Lemma:
- Theorem Every uniform space is completely regular (as a topological space with the topology induced by the uniformity).
Remark This only means that there is a continuous function ![\ f : X \rightarrow [0;1]](../w/images/math/0/f/9/0f9c03bc23bc310dd7ad44fd0bbc5274.png) such that
such that 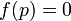 and
and 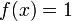 for every
for every 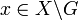 , whenever
, whenever 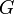 is a neighborhood of
is a neighborhood of 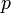 . However, it does not mean that uniform spaces have to be Hausdorff spaces. In fact, uniform space with the weakest uniformity has the weakest topology, hence it's never Hausdorff, not even T0, unless it has no more than one point.
. However, it does not mean that uniform spaces have to be Hausdorff spaces. In fact, uniform space with the weakest uniformity has the weakest topology, hence it's never Hausdorff, not even T0, unless it has no more than one point.
On the other hand, when one of any two points has a neighborhood to which the other one does not belong then the two 1-point sets, consisting of these two points, are apart, hence they admit disjoint neighborhoods. Thus it is easy to prove the following:
- Theorem The following three topological properties of a uniform space
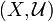 are equivalent
are equivalent
-
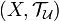 is a T0-space;
is a T0-space;
-
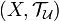 is a T2-space (i.e. Hausdorff);
is a T2-space (i.e. Hausdorff);
-
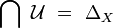 .
.
-
When a uniform structure induces a Hausdorff topology then it's called separating.
[edit] Uniform continuity and uniform homeomorphisms
Let 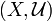 and
and 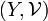 be uniform spaces. Function
be uniform spaces. Function 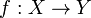 is called uniformly continuous if
is called uniformly continuous if
A more elementary calculus δε-like equivalent definition would sound like this (UV play the role of δε respectively):
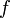 is uniformly continuous if (and only if) for every
is uniformly continuous if (and only if) for every 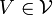 there exists
there exists 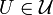 such that for every
such that for every 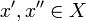 if
if 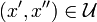 then
then 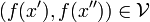 .
.
Every uniformly continuous map is continuous with respect to the topologies induced by the involved uniform structures.
Example Every constant map from one uniform space to another is uniformly continuous.
A uniformly continuous map 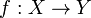 of a uniform space
of a uniform space 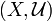 into a uniform space
into a uniform space 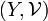 is called a uniform homeomorphism (of these two spaces) if it is bijective, and the inverse function
is called a uniform homeomorphism (of these two spaces) if it is bijective, and the inverse function 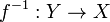 is a uniformly continuous map of
is a uniformly continuous map of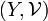 into
into 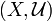 .
.
[edit] Constructions and operations
Constructions of new uniform spaces based on already existing uniform spaces are called operations. Otherwise they are called simply constructions. Thus the uniformity induced by a metric (see above) is an example of a construction (of a uniformity).
A full conceptual appreciation of operations and constructions requires the theory of categories (see below).
[edit] Partial order of uniformities
The set of uniform structures in a set  is (partially) ordered by the inclusion relation; given two uniformities
is (partially) ordered by the inclusion relation; given two uniformities 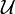 and
and 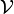 in
in  such that
such that 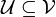 we say that
we say that 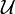 is weaker than
is weaker than 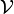 and
and 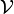 is stronger than
is stronger than 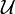 . The set of all uniform structures in
. The set of all uniform structures in  has the weakest (smallest) and the strongest (largest) element (uniformity). We will see in the next section, that each set of uniform structures in
has the weakest (smallest) and the strongest (largest) element (uniformity). We will see in the next section, that each set of uniform structures in  admits the least upper bound. Thus it follows that each set admits also the greatest lower bound—indeed, the weakest uniformity is one of the lower bounds of a set, and there exists the least upper bound of the set of all lower bounds, which is the required greatest lower bound. In short, the uniformities in arbitrary set
admits the least upper bound. Thus it follows that each set admits also the greatest lower bound—indeed, the weakest uniformity is one of the lower bounds of a set, and there exists the least upper bound of the set of all lower bounds, which is the required greatest lower bound. In short, the uniformities in arbitrary set  form a complete Birkhoff lattice.
form a complete Birkhoff lattice.
[edit] The least upper bound
Let 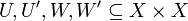 be such that:
be such that:
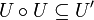 and
and 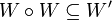
Then
The same holds not just for two but for any finite (or just arbitrary) family of pairs 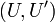 as above.
as above.
Let 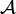 be an arbitrary family of uniformities in
be an arbitrary family of uniformities in  . We construct the least upper bound of such a family. The union of uniformities is in general not an uniformity, since it is not closed under intersections. Taking this fact into account, we consider all finite intersections of entourages belonging to the union of all uniformities of
. We construct the least upper bound of such a family. The union of uniformities is in general not an uniformity, since it is not closed under intersections. Taking this fact into account, we consider all finite intersections of entourages belonging to the union of all uniformities of 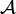 . These intersections form a base
. These intersections form a base 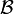 of a uniformity
of a uniformity 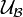 ; the latter is the least upper bound of
; the latter is the least upper bound of 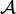 :
:
[edit] Preimage
Let  be a set; let
be a set; let 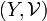 be a uniform space; let
be a uniform space; let 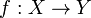 be an arbitrary function. Then
be an arbitrary function. Then
is a base of a uniform structure 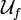 in
in  . Uniformity
. Uniformity 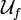 is called the preimage of uniformity
is called the preimage of uniformity 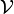 under function
under function 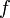 . Now
. Now 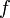 became a uniformly continuous map of the uniform space
became a uniformly continuous map of the uniform space 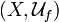 into
into 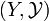 . Moreover, and that's the whole point of the preimage operation, uniformity
. Moreover, and that's the whole point of the preimage operation, uniformity 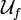 is the weakest in
is the weakest in  , with respect to which function
, with respect to which function 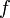 is uniformly continuous.
is uniformly continuous.
- Let
 be a set; let
be a set; let 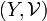 be a uniform space; let
be a uniform space; let 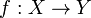 be an arbitrary surjection. Then for every uniform space
be an arbitrary surjection. Then for every uniform space 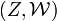 , and every function
, and every function 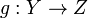 such that
such that 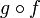 is a uniformly continuous map of
is a uniformly continuous map of 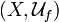 into
into 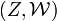 , the function
, the function 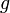 is a uniformly continuous map of
is a uniformly continuous map of 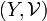 into
into 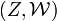 .
.
The preimage uniformity can be characterized purely in terms of function; thus the following theorem could be a (non-constructive) definition of the preimage uniformity:
Theorem Let  be a set; let
be a set; let 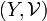 be a uniform space; let
be a uniform space; let 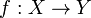 be an arbitrary function. The preimage uniformity is the only uniform structure
be an arbitrary function. The preimage uniformity is the only uniform structure 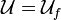 which satisfies the following two conditions:
which satisfies the following two conditions:
-
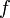 is a uniformly continuous map of
is a uniformly continuous map of 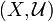 into
into 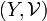 ;
;
- for every uniform space
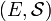 , and for every function
, and for every function 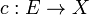 , if
, if 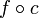 is a uniformly continuous map of
is a uniformly continuous map of 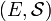 , into
, into 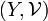 , then
, then  is a uniformly continuous map of
is a uniformly continuous map of 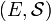 into
into 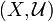 .
.
Proof The first condition means that 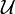 is stronger than the preimage
is stronger than the preimage 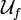 ; and the second condition, once we substitute
; and the second condition, once we substitute 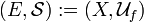 ,
and
,
and 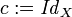 , tells us that
, tells us that 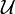 is weaker than
is weaker than 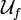 . Thus
. Thus 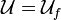 . Of course
. Of course 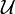 satisfies both conditions of the theorem.
satisfies both conditions of the theorem.
End of proof.
[edit] Uniform subspace
Let 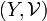 be a uniform space; let
be a uniform space; let  be a subset of
be a subset of 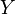 . Let uniformity
. Let uniformity 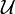 be the primage of uniformity
be the primage of uniformity 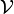 under the identity embedding
under the identity embedding 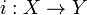 (where
(where 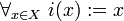 ). Then
). Then 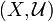 is called the uniform subspace of the uniform space
is called the uniform subspace of the uniform space 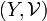 , and
, and 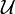 – the subspace uniformity. It is directly described by the equality:
– the subspace uniformity. It is directly described by the equality:
The subspace uniformity is the weakest in  under which the embedding
under which the embedding 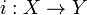 is uniformly continuous.
is uniformly continuous.
The following theorem is a characterization of the subspace uniformity in terms of functions (it is a special case of the theorem about the preimage structure; see above):
Theorem Let 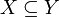 , where
, where 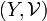 is a uniform space. The subspace uniformity is the only uniform structure
is a uniform space. The subspace uniformity is the only uniform structure 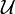 in
in  which satisfies the following two conditions:
which satisfies the following two conditions:
- the identity embedding
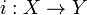 is a uniformly continuous map of
is a uniformly continuous map of 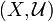 into
into 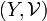 ;
;
- for every uniform space
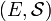 , and for every function
, and for every function 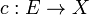 , if
, if 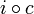 is a uniformly continuous map of
is a uniformly continuous map of 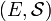 into
into 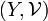 , then
, then  is a uniformly continuous map of
is a uniformly continuous map of 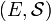 into
into 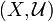 .
.
[edit] Uniform (Cartesian) product
Let 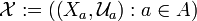 be an indexed family of uniform spaces. Let
be an indexed family of uniform spaces. Let 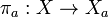 be the standard projection of the cartesian product
be the standard projection of the cartesian product
onto 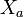 , for every
, for every 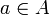 . Then the least upper bound of the preimage uniformities:
. Then the least upper bound of the preimage uniformities:
is called the product uniformity in  , and
, and 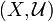 is called the product of the family of uniform spaces
is called the product of the family of uniform spaces 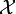 . Thus the product uniformity is the weakiest under which the standard projections are uniform. It is characterized in terms of functions as follows:
. Thus the product uniformity is the weakiest under which the standard projections are uniform. It is characterized in terms of functions as follows:
Theorem The product uniformity 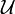 (see above) is the only one in the Cartesian product
(see above) is the only one in the Cartesian product  , which satisfies the following two conditions:
, which satisfies the following two conditions:
- each projection
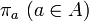 is a uniformly continuous map of
is a uniformly continuous map of 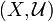 into
into 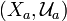 ;
;
- for every uniform space
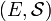 , and for every (indexed) family of uniformly continuous maps
, and for every (indexed) family of uniformly continuous maps 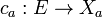 , of
, of 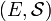 into
into 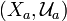 (for
(for 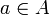 ) there exists exactly one uniformly continuous map
) there exists exactly one uniformly continuous map 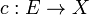 such that:
such that:
Remark The theory of sets tells us that the unique uniformly continuous map  is, as a function, the diagonal product:
is, as a function, the diagonal product:
Thus the above theorem really says that the diagonal product of uniformly continuous maps is uniformly continuous.
Remark In many texts the diagonal product, 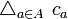 , is called incorrectly the Cartesian product of functions,
, is called incorrectly the Cartesian product of functions, 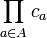 ; the correct terminology is used for instance in "Outline of General Topology" by Ryszard Engelking.
; the correct terminology is used for instance in "Outline of General Topology" by Ryszard Engelking.
[edit] The category of the uniform spaces
The identity function 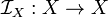 , which maps every point onto itself, is a uniformly continuous map of
, which maps every point onto itself, is a uniformly continuous map of 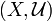 onto itself, for every uniform structure
onto itself, for every uniform structure 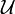 in
in  .
.
Also, if 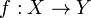 and
and 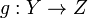 are uniformly continuous maps of
are uniformly continuous maps of 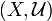 into
into 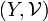 , and of
, and of 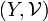 into
into 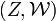 respectively, then
respectively, then 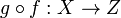 is a uniformly continuous map of
is a uniformly continuous map of 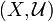 into
into  .
.
These two properties of the uniformly continuous maps mean that the uniform spaces (as objects) together with the uniform maps (as morphisms) form a category 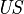 (for Uniform Spaces).
(for Uniform Spaces).
Remark A morphism in category 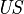 is more than a function; it is an ordered triple consisting of two objects (domain and range) and one function (but it must be uniformly continuous). This means that one and the same function may serve more than one morphism in
is more than a function; it is an ordered triple consisting of two objects (domain and range) and one function (but it must be uniformly continuous). This means that one and the same function may serve more than one morphism in 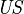 , if a function is defined as just a graph. However, also a function is often defined as consisting of domain, codomain and graph.
, if a function is defined as just a graph. However, also a function is often defined as consisting of domain, codomain and graph.
[edit] Pointers
Pointers play a role in the theory of uniform spaces which is similar to the role of Cauchy sequences of points, and of the Cantor decreasing sequences of closed sets (whose diameters converge to 0) in mathematical analysis. First let's introduce auxiliary notions of neighbors and clusters.
[edit] Neighbors
Let 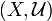 be a uniform space. Two subsets
be a uniform space. Two subsets 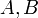 of
of 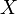 are called neighbors – and then we write
are called neighbors – and then we write 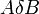 – if:
– if:
for arbitrary 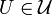 .
.
- Either
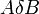 or there exists an entourage
or there exists an entourage 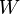 such that
such that 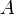 and
and 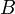 are
are 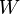 -apart.
-apart.
If more than one uniform structure is present then we write 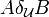 in order to specify the structure in question.
in order to specify the structure in question.
The neighbor relation enjoys the following properties:
- no set is a neighbor of the empty set;
-

-
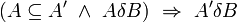
-
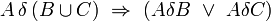
-
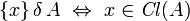
-
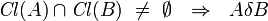
for arbitrary  and
and 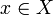 .
.
Remark Relation 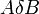 , and a set of axioms similar to the above selection of properties of
, and a set of axioms similar to the above selection of properties of 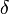 , was the start point of the Efremovich-Smirnov approach to the topic of uniformity.
, was the start point of the Efremovich-Smirnov approach to the topic of uniformity.
Also:
- if
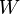 is an entourage,
is an entourage, 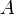 and
and 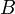 are both
are both 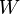 -sets, and
-sets, and 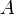 and
and 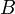 are neighbors, then the union
are neighbors, then the union 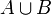 is a
is a 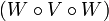 -set for every entourage
-set for every entourage 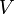 ; in particular, it is a
; in particular, it is a 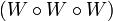 -set.
-set.
Furthermore, if 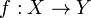 is a uniformly continuous map of
is a uniformly continuous map of 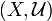 into
into 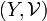 , then
, then
for arbitrary 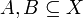 .
.
[edit] Clusters
Let 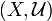 be a uniform space. A family
be a uniform space. A family 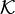 of subsets of
of subsets of 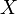 is called a cluster if each two members of
is called a cluster if each two members of 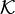 are neighbors.
are neighbors.
- Every subfamily of a cluster is a cluster.
- If every member of a cluster is a
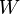 -set, then its union is a
-set, then its union is a 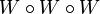 -set.
-set.
- If
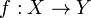 is a uniformly continuous map of
is a uniformly continuous map of 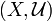 into
into 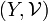 , and
, and 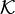 is a cluster in
is a cluster in 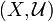 , then
, then
is a cluster in 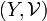 .
.
[edit] Pointers
A cluster 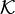 in a uniform space
in a uniform space 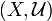 is called a pointer if for every entourage
is called a pointer if for every entourage 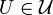 there exists a
there exists a 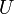 -set
-set 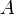 (meaning
(meaning 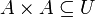 ) such that
) such that
If 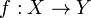 is a uniformly continuous map of
is a uniformly continuous map of 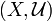 into
into 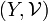 , and
, and 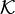 is a pointer in
is a pointer in 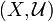 , then
, then
is a pointer in 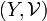 .
.
- Every base of neighborhoods of a point is a pointer. Thus the filter of all neighborhoods of a point is called the pointer of neighborhoods (of the given point).
[edit] Equivalence of pointers, maximal and minimal pointers
Let the elunia of two families 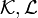 , be the family
, be the family 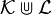 of the unions of pairs of elements of these two families, i.e.
of the unions of pairs of elements of these two families, i.e.
Definition Two pointers 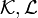 are called equivalent if their
are called equivalent if their 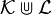 elunia is a pointer,
in which case we write
elunia is a pointer,
in which case we write 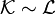 .
.
This is indeed an equivalence relation: reflexive, symmetric and transitive.
- Two pointers are equivalent if and only if their union is a pointer.
- The union of all pointers equivalent with a given one is a pointer from the same equivalence class. Thus each equivalent class of pointers has a pointer which contains every pointer of the given class. The following three properties of a pointer
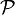 in a uniform space
in a uniform space 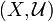 are equivalent:
are equivalent:
- if
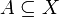 is a neighbor of every member of
is a neighbor of every member of 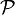 then
then 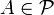 ;
;
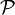 is not contained in any pointer different from itself;
is not contained in any pointer different from itself;
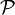 contains every pointer equivalent to itself.
contains every pointer equivalent to itself.
- if
- Let
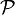 be a pointer in
be a pointer in 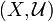 . Let
. Let
for every entourage 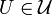 . Then
. Then 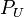 is a
is a 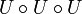 -set. It follows that
-set. It follows that
is a pointer equivalent to 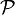 .
.
- Let's call a pointer
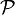 upward full if it has every superset
upward full if it has every superset 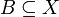 of each of its members
of each of its members 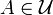 . If
. If 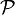 is an arbitrary pointer, then its upward fulfillment
is an arbitrary pointer, then its upward fulfillment
is an upward full pointer equivalent to 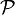 .
.
- Let
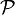 be a pointer which is maximal in its equivalence class. Let
be a pointer which is maximal in its equivalence class. Let 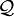 be the pointer defined above. Let
be the pointer defined above. Let 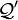 be its upward fulfillment. Pointer
be its upward fulfillment. Pointer 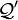 is the the unique upward full pointer of its class, which is contained in any other upward full pointer of this class.
is the the unique upward full pointer of its class, which is contained in any other upward full pointer of this class.
We see that each equivalent class of pointers has two unique pointers: one maximal in the whole class, and one minimal among all upward full pointers.
[edit] Convergent pointers
A pointer 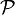 in a uniform space is said to point to point
in a uniform space is said to point to point 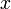 if it is equivalent to the pointer of the neighborhoods of
if it is equivalent to the pointer of the neighborhoods of 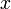 . When a pointer points to a point then we say that such a pointer id convergent.
. When a pointer points to a point then we say that such a pointer id convergent.
- A uniform space is Hausdorff (as a topological space) if and only if no pointer converges to more than one point.
[edit] Complete uniform spaces and completions
A uniform space is called complete if each pointer of this space is convergent.
Remark In mathematical practice (so far) only Hausdorff complete uniform spaces play an important role; it must be due to the fact that in Hausdorff spaces each pointer points to at the most one point, and to exactly one in the case of a Hausdorff complete space.
For every uniform space 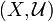 its completion is defined as a uniform map
its completion is defined as a uniform map 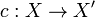 of
of 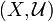 into a Hausdorff complete space
into a Hausdorff complete space 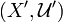 , which has the following universality property:
, which has the following universality property:
- for every uniform map
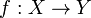 of
of 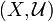 into a Hausdorff complete space
into a Hausdorff complete space 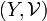 there exists exactly one uniform map
there exists exactly one uniform map 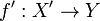 of
of 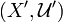 into
into 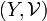 such that
such that 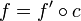 .
.
Theorem For every uniform space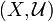 there exists a completion
there exists a completion 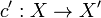 of
of 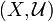 into a Hausdorff complete space
into a Hausdorff complete space 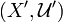 . Such a completion is unique up to a uniform homeomorphism, meaning that if
. Such a completion is unique up to a uniform homeomorphism, meaning that if 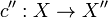 is another completion of
is another completion of 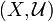 into a Hausdorff complete space
into a Hausdorff complete space 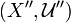 . then there is exactly one uniform homeomorphism
. then there is exactly one uniform homeomorphism 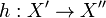 such that
such that 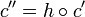 .
.
Remark The second part of the theorem, about the uniqueness of the completion (up to a uniform homeomorphism) is an immediate consequence of the definition of the completion (it has a uniqueness statement as its part).
| |
Some content on this page may previously have appeared on Citizendium. |