Triangle inequality
The triangle inequality is a basic result in mathematics, which, in its simplest form, can be stated in words as follows:
- The sum of the lengths of two sides of a triangle is greater than the length of the third.
It is based on the intuitive idea that:
- The straight line path is the shortest path.
The former statement is often taught to students at the end of primary school or the beginning of middle school. The triangle inequality comes up in a number of other forms throughout mathematics, and is encountered in the theory of metric spaces in topology, the theory of normed vector spaces in functional analysis, and in parts of complex analysis.
Contents |
[edit] In Euclidean geometry
[edit] Formal statement
In Euclidean geometry, the statement is as follows:
Let A,B,C be three non-collinear points in the plane. Then, we have:
| AB | + | BC | > | AC |
where  denotes the length of the line segment joining the two points.
denotes the length of the line segment joining the two points.
If we consider the triangle 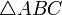 , then this is precisely the statement that the sum of two sides of a triangle is greater than the third.
, then this is precisely the statement that the sum of two sides of a triangle is greater than the third.
When A,B,C are collinear, we get what is called a degenerate triangle. For degenerate triangles, equality can hold. It holds iff B is between A and C.
[edit] Intuitive justification
The rationale behind the triangle inequality is that the straight line path from A to C is shorter than the path where we first go to B, and then to C.
[edit] In metric spaces
A metric space is a mathematical abstraction of spaces with a notion of distance between any two points. Since the triangle inequality is so fundamental to the way we expect distance to behave, the triangle inequality is assumed as one of the axioms for a metric space. Formally, a metric space is a set X equipped with a distance function 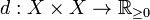 that satisfies the following conditions for all points
that satisfies the following conditions for all points 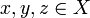 :
:
- d is symmetric i.e. d(x,y) = d(y,x)
- d(x,y) > 0 if
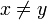 and d(x,y) = 0 if x = y
and d(x,y) = 0 if x = y
-
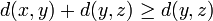
| |
Some content on this page may previously have appeared on Citizendium. |

