Sturm-Liouville theory/Proofs
This article proves that solutions to the Sturm-Liouville equation corresponding to distinct eigenvalues are orthogonal. Note that when the Sturm-Liouville problem is regular, distinct eigenvalues are guaranteed. For background see Sturm-Liouville theory.
[edit] Orthogonality Theorem
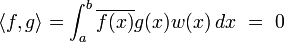, where f(x) and g(x) are solutions to the Sturm-Liouville equation corresponding to distinct eigenvalues and w(x) is the "weight" or "density" function.
[edit] Proof
Let f(x) and g(x) be solutions of the Sturm-Liouville equation (1) corresponding to eigenvalues λ and μ respectively. Multiply the equation for g(x) by f(x) (the complex conjugate of f(x)) to get:
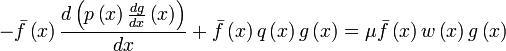
(Only f(x), g(x), λ, and μ may be complex; all other quantities are real.) Complex conjugate this equation, exchange f(x) and g(x), and subtract the new equation from the original:
![-\bar{f} \left( x\right) \frac{d\left( p\left( x\right) \frac{dg}{dx}
\left( x\right) \right) }{dx} +g\left( x\right) \frac{d\left( p\left(
x\right) \frac{d\bar{f} }{dx} \left( x\right) \right) }{dx} =\frac{d\left(
p\left( x\right) \left[ g\left( x\right) \frac{d\bar{f} }{dx} \left(
x\right) -\bar{f} \left( x\right) \frac{dg}{dx} \left( x\right) \right]
\right) }{dx} =\left( \mu -\bar{\lambda} \right) \bar{f} \left( x\right)
g\left( x\right) w\left( x\right)](../../w/images/math/3/6/b/36b52df51428c7db35e9e8a34ec0b00e.png)
Integrate this between the limits
x = a
and
x = b
![\left( \mu -\bar{\lambda} \right) \int\nolimits_{a}^{b}\bar{f} \left(
x\right) g\left( x\right) w\left( x\right) dx =p\left( b\right) \left[
g\left( b\right) \frac{d\bar{f} }{dx} \left( b\right) -\bar{f} \left( b\right)
\frac{dg}{dx} \left( b\right) \right] -p\left( a\right) \left[ g\left(
a\right) \frac{d\bar{f} }{dx} \left( a\right) -\bar{f} \left( a\right)
\frac{dg}{dx} \left( a\right) \right]](../../w/images/math/a/3/8/a38902d7b6ff300a12464d1d3e7ee087.png)
.
The right side of this equation vanishes because of the boundary conditions, which are either:
-
periodic boundary conditions, i.e., that f(x), g(x), and their first derivatives (as well as p(x)) have the same values at x = b as at x = a, or
- that independently at x = a and at x = b either:
So: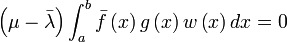 
If we set f = g , so that the integral surely is non-zero, then it follows that λ =λ that is, the eigenvalues are real, making the differential operator in the Sturm-Liouville equation self-adjoint (hermitian); so:
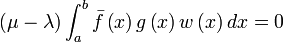
It follows that, if f and g have distinct eigenvalues, then they are orthogonal. QED.
|
Some content on this page may previously have appeared on Citizendium. |
