Simon Stevin
Contents |
Simon Stevin (1548 – 1620) was a Flemish-Dutch engineer and mathematician, who was the first to write rational numbers as decimal fractions. He was also the first to decompose forces by using geometric drawings that are equivalent to what we now call "the parallelogram of forces" (see vector addition) and he performed experiments that refuted Aristotle's law of free fall—he did this a few years before Galileo Galilei reputedly did similar experiments. That is, Stevin found that heavy bodies do not fall faster than light ones.[1] Stevin excelled in mathematical theory and engineering applications.
[edit] Life
Simon Stevin was born in Bruges, one of the important cities of Flanders, the Dutch speaking part of the present-day country Belgium. He was a natural child of Antheunis Stevin and Cathelyne van der Poort. He worked as a merchant's bookkeeper in Antwerp, the largest city in Flanders, and later as financial clerk in the administration of the Vrije van Brugge, the rural district surrounding Bruges.
For unclear reasons he moved around 1580 to Leiden in the The Netherlands; it is improbable that his migration was for religious reasons, for he was remarkably indifferent to religious matters. He registered as a student in the University of Leiden on February 16th, 1583 and started a career as engineer and applied mathematician. Simon Stevin had four children. As to his marriage we only know of a notice of marriage with Catherina Cray at Leyden on April 10th 1616, when he was 68 years old (Simon Stevin had four children with Catherina, two sons and two daughters, all born before the parents were officially married). Stevin died in 1620; the exact date nor the place is known but he passed away between February 20th and April 8th and most probably in The Hague, where he had bought a house in 1612.
[edit] Work
While still in Flanders, Stevin composed world's first table of interests Tafelen van Interest (1582) in which he set out the rules for the computation of interest and gave useful tables (which were kept secret by the banking houses of the time). Two years later (1584) his Problematica Geometrica came from the press in Antwerp.
In 1585 (the year that Antwerp was recaptured by the Spanish) Stevin published in Leiden a booklet, De Thiende [The Tenth], in which he presented an elementary account of decimal fractions and their daily use. His booklet starts with:
Den Sterrekyckers, Landt meters, Tapijtmeters, Wijnmeters, Lichaemmeters int ghemeene, Muntmeesters, ende allen Cooplieden, wenscht Simon Stevin Gheluck.
[Simon Stevin wishes luck to Stargazers, Surveyors, Carpet-measurers, Wine-gaugers, Stereometers in general, Mintmasters and all Merchants.]
making clear that he had very practical applications in mind with his new arithmetic tool. Although the idea of decimal fractions was already in existence and Stevin's notation was rather unwieldy (he did not yet use the decimal point as place holder but wrote an encircled power of ten after each digit in the fraction), he established and popularized their use in day-to-day mathematics. Robert Norton published an English translation of De Thiende in London in 1608. It was entitled Disme, the Arts of Tenths or Decimall Arithmetike. It is this work that inspired Thomas Jefferson, Benjamin Franklin, Alexander Hamilton, and the first mint master David Rittenhouse to deviate from the British currency system and to propose a decimal currency for the United States, a country that otherwise uses the imperial system for its units. (One tenth of a dollar is a dime; the name is derived from disme).
In 1585 Stevin published L'arithmétique. In it Stevin presented a unified treatment for solving quadratic equations and a method for finding approximate solutions to algebraic equations of all degrees. He considered all kinds of real numbers on an equal footing—natural numbers, roots (the majority of which are irrational numbers), and negative numbers. He did not accept complex numbers.
Stevin's most important work: De beghinselen der weeghconst [The principles of the art of weighing] appeared in in 1586. By weeghconst Stevin means the part of mechanics that is called statics. This field was founded by Archimedes and Stevin continued his theoretical work on the forces that keep solid bodies in their place. Stevin treats a solid body on a sloping plane and decomposes the gravitational force in a component perpendicular to the plane and one that keeps the body in rest on the slope; doing this he introduced the "the parallelogram of forces". See the figure for a practical application.
The year 1586 was very fruitful for Stevin. In that year he also published Beghinselen des Waterwichts (Elements of Hydrostatics) in which he established the Archimedean principle in a more elementary and therefore more satisfactory manner than Archimedes himself had done. Stevin was the first to evaluate the forces that a liquid exerts by its weight on the walls of a vessel.
In the same year (1586) Stevin published a report on his experiment performed in Delft together with Johan Cornets de Groot, the burgomaster of Delft and father of Hugo Grotius. They dropped two equally sized balls, one 10 times as heavy as the other, from a church tower. After falling a distance of 30 feet, the balls landed on a wooden plank. The two observers heard one bang only and concluded that the two balls fell with equal speed. Reputedly, Galileo Galilei performed similar experiments during his post in Pisa (1589–1592).
In the second half of the 1580s Stevin applied for patents for several civil engineering inventions, such as improvements for windmills used for drainage.
In 1594 appeared the Appendice Algebraïque, an eight-page pamphlet. In it he gave a numerical method for solution of algebraic equations of any degree by means of successive approximations. The only extant copy of this work was lost in the fire of the library of the University of Leuven that was set by the German army (28 August, 1914).
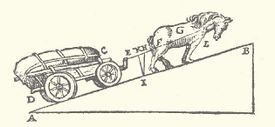
Around 1590 Stevin became adviser and tutor in mathematics and natural sciences of the Stadtholder Maurice, Prince of Orange, who had succeeded his father William the Silent as leader of the Dutch Revolt and commander-in-chief of the State army. Stevin instructed Maurice in various subjects and wrote teaching material for him that later was published in Wisconstighe Ghedachtenissen [Mathematical Memoirs] (1605-1608). He constructed for Maurice a famous sailing-carriage holding 28 passengers, (see the figure) that on the flat Dutch beach could cover the distance from Scheveningen to Petten (85 km) in two hours.[2] [3] A sustained speed of more than 40 km/h was incredible in those days. Also for Maurice he wrote in 1594 Stercktenbouwing (the building of fortifications).
Upon invitation of the city of Dantzig (Gdansk) he traveled to Poland in the summer of 1591, probably to give advise about Dantzig's harbor.
In 1600 Stevin was asked to compose an instruction for a new school of engineers connected to Leiden university. The new course was written in Dutch so that also students who did not know Latin could follow it.
Stevin wrote on astronomy and defended the sun-centered system of Copernicus in De Hemelloop (the course of heaven), that appeared in 1608 as part of the Wisconstighe Ghedachtenissen. Stevin's Copernicanism met some resistance from influential Calvinist theologians, such as Ubbo Emmius, but this resistance was uncomparable to the heavy-handed censoring experienced eight years later by Galileo, who shared Stevin's Copernicanism.
Stevin loved the Dutch language and was a purist. He invented many words that are still current in Dutch (a famous example is wisconst for mathematics, in modern Dutch wiskunde—literally the art of certainties; wisconstigh means mathematical). After the mid 1590s he did no longer write in any other language than Dutch, which gave him a lower international profile than a man of his talents deserved.
[edit] Notes
- ↑ This is only strictly true in vacuum. The upward force due to friction with air is relatively stronger for light bodies than for heavy bodies; a lead ball drops faster in air than an air-filled balloon, even when both have the same diameter.
- ↑ Twenty year-old Hugo Grotius, who made the trip, wrote a Latin poem about it, see Google books for the Latin original and a very free translation into Dutch (1846).
- ↑ A. J. Kox in Van Stevin tot Lorentz, Intermediair Bibliotheek, Amsterdam (1980) calls the story of the two hour trip strongly exaggerated. If one considers the amount of sail, the weight of 28 persons, the softness of the sandy beach even at low tide, and the absence of pneumatic tires, a speed of 40 km/h indeed seems high.
[edit] External links
- StevinEngels.html Private webpage about Stevin, partly in Dutch. Last visited April 15, 2011.
- Biography by K. van Berkel (in English, pdf).