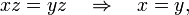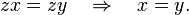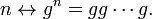Semigroup
In algebra, a semigroup is a set equipped with a binary operation satisfying certain properties similar to but less stringent than those of a group. A motivating example of a semigroup is the set of positive integers with multiplication as the operation.
Formally, a semigroup is a set S with a binary operation  satisfying the following conditions:
satisfying the following conditions:
- S is closed under
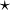 ;
;
- The operation
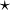 is associative.
is associative.
A commutative semigroup is one which satisfies the further property that 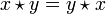 for all x and y in S. Commutative semigroups are often written additively.
for all x and y in S. Commutative semigroups are often written additively.
A subsemigroup of S is a subset T of S which is closed under the binary operation and hence is again a semigroup.
A semigroup homomorphism f from semigroup 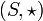 to
to 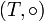 is a map from S to T satisfying
is a map from S to T satisfying
Contents |
[edit] Examples
- The positive integers under addition form a commutative semigroup.
- The positive integers under multiplication form a commutative semigroup.
- Square matrices under matrix multiplication form a semigroup, not in general commutative.
- Every monoid is a semigroup, by "forgetting" the identity element.
- Every group is a semigroup, by "forgetting" the identity element and inverse operation.
[edit] Congruences
A congruence on a semigroup S is an equivalence relation 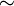 which respects the binary operation:
which respects the binary operation:
The equivalence classes under a congruence can be given a semigroup structure
and this defines the quotient semigroup 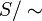 .
.
[edit] Cancellation property
A semigroup satisfies the cancellation property if
A semigroup is a subsemigroup of a group if and only if it satisfies the cancellation property.
[edit] Free semigroup
The free semigroup on a set G of generators is the set of all "words" on G (that is, the finite sequences of elements of G) with the binary operation being concatenation (juxtaposition). The free semigroup on one generator g may be identified with the semigroup of positive integers under addition
Every semigroup may be expressed as a quotient of a free semigroup.
| |
Some content on this page may previously have appeared on Citizendium. |


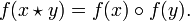
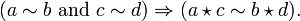
![[x] \circ [y] = [x \star y] \,](../w/images/math/a/8/1/a811eba2f02f756f3ec1e0941f397a30.png)