Scientific notation
Scientific notation is a method of representing numbers compactly. It is most useful when working with very small and very large numbers, though it is applicable to any real number. A number in scientific notation is expressed as a number between -10 and 10 multiplied by 10 raised to a power, 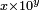 . For example, the number 325,000,000 is expressed as 3.25 × 108. (In computer programming use, and in many spreadsheet programs, the multiplication symbol and the 10 are replaced by an E: 3.25 E+8 for 3.25 × 108.)
. For example, the number 325,000,000 is expressed as 3.25 × 108. (In computer programming use, and in many spreadsheet programs, the multiplication symbol and the 10 are replaced by an E: 3.25 E+8 for 3.25 × 108.)
To convert a number from ordinary decimal notation to scientific notation, the number is divided by the largest power of 10 smaller than (or equal to) the absolute value of the number, to obtain the coefficient; the exponent is the radix of the power of 10. If the number is negative, a minus sign is placed to the left of the number as a whole. If the number is between -1 and 1, the power of ten is negative, and a minus sign appears in the exponent. Thus 0.04321 in scientific notation is 4.321 × 10-2, while -23.14069 is -2.314069 × 101.
Numbers in scientific notation are often truncated to the number of significant figures available for the number or required for the computation; thus the speed of light in a vacuum, which is defined as 299,792,458 m/s, is expressed as 3.00 × 108, where only two significant figures are required. Trailing zeros are considered significant in scientific notation, while in ordinary decimal notation, the number of significant figures is often unclear. For example, the population of New Castle County, Delaware at the 2000 census was 500,265. If this is approximated as 500,000, it is unclear how many of the zeros are significant; while expressing the number as 5.00 × 105 clearly indicates that there are three significant figures in the approximation.
Engineering notation is a variant of scientific notation popular on some brands of calculators, where instead of using the nearest power of 10, the nearest power of 1000 is used, though the number is still expressed as a coefficient multiplied by a power of ten. Thus, for example, the number 325,000,000 is expressed as 325. × 106. This variant of the notation is useful for comparing numbers which range over a few orders of magnitude, and for use with SI scale prefixes.
| |
Some content on this page may previously have appeared on Citizendium. |

