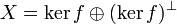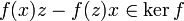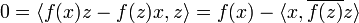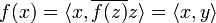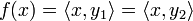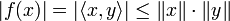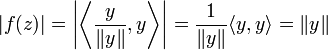Riesz representation theorem
[edit] Theorem
Let f be a bounded linear functional in a Hilbert space X over 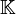 . Then there exists a unique
. Then there exists a unique 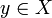 such that, for all
such that, for all 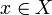 ,
,
and
[edit] Proof
If f = 0 take y = 0. Suppose then that 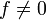 and consider kerf, which is a closed space by this proposition. By the Hilbert space decomposition theorem we then have
and consider kerf, which is a closed space by this proposition. By the Hilbert space decomposition theorem we then have
and, since 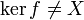 ,
, 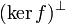 has an element z such that
has an element z such that  . Note now that, for all
. Note now that, for all 
and, since 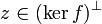 ,
,
that is to say
with 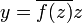 .
To prove uniqueness, suppose that for all
.
To prove uniqueness, suppose that for all 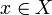
for some two elements 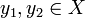 .
Then
.
Then 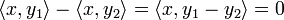 for all
for all 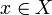 . In particular, for x = y1 − y2 which would imply
. In particular, for x = y1 − y2 which would imply 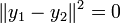 and hence y1 = y2.
Finally, since the inner product is continuous on the first variable
and hence y1 = y2.
Finally, since the inner product is continuous on the first variable
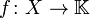 ,
, 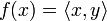
is a linear functional that is continuous, and hence bounded by the bounded operator equivalence theorem. Applying the Cauchy-Schwarz inequality, we get
and so 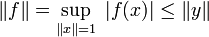 . If y = 0 then
. If y = 0 then 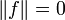 so f = 0. If not, consider
so f = 0. If not, consider 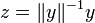 to obtain
to obtain
which yields 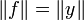 .
.
| |
Some content on this page may previously have appeared on Bourbawiki. |