Riemann-Roch theorem
In algebraic geometry the Riemann-Roch theorem states that if C is a smooth algebraic curve, and 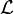 is an invertible sheaf on C then the the following properties hold:
is an invertible sheaf on C then the the following properties hold:
- The Euler characteristic of
 is given by
is given by 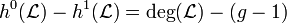
- There is a canonical isomorphism
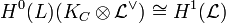
Contents |
[edit] Some examples and applications
The examples we give arise from considering complete linear systems on curves.
- Any curve C of genus 0 is isomorphic to the projective line: Indeed if p is a point on the curve then h0(p) − 0 = 1 − (0 − 1) = 2; hence the map
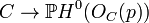 is a degree 1 map, or an isomorphism.
is a degree 1 map, or an isomorphism.
- Any curve of genus 1 is a double cover of a projective line: Indeed if p is a point on the curve then h0(2p) − 0 = 2 − (1 − 1) = 2; hence the map
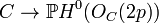 is a degree 2 map.
is a degree 2 map.
- Any curve of genus 2 is a double cover of a projective line: Indeed the degree of the canonical class KC is 2g − 2 and therefore h0(KC) − h0(OC) = 2 − (2 − 1) = 1; since h0(OC) = 1 the map
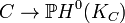 is a degree 2 map.
is a degree 2 map.
- The Riemann-Hurwitz formula.
[edit] Geometric Riemann-Roch
From the statement of the theorem one sees that an effective divisor D of degree d on a curve C satisfies h0(D) > d − (g − 1) if and only if there is an effective divisor D' such that D + D'∼KC in Pic(C). In this case there is a natural isomorphism![\{[H]\in|K_C|, H\cdot C=D'\}\cong\mathbb{P}H^0(D)](../w/images/math/9/7/1/97168840bb68a22ceb31cff3bbc85cd9.png) , where we identify C with it's image in the dual canonical system | KC | * .
, where we identify C with it's image in the dual canonical system | KC | * .
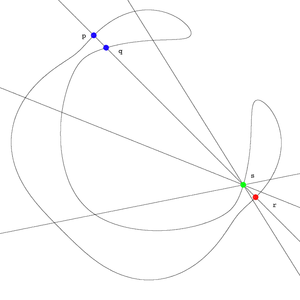
As an example we consider effective divisors of degrees 2,3 on a non hyperelliptic curve C of genus 3. The degree of the canonical class is 2genus(c) − 2 = 4, whereas h0(KC) = 2genus(C) − 2 − (genus(C) − 1) + h0(0) = g. Hence the canonical image of C is a smooth plane quartic. We now idenitfy C with it's image in the dual canonical system. Let p,q be two points on C then there are exactly two points
r,s such that 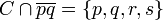 , where we intersect with multiplicities, and if p = q we consider the tangent line TpC instead of the line
, where we intersect with multiplicities, and if p = q we consider the tangent line TpC instead of the line 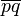 . Hence there is a natural isomorphism between
. Hence there is a natural isomorphism between 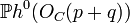 and the unique point in | KC | representing the line
and the unique point in | KC | representing the line 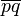 . There is also a natural ismorphism between
. There is also a natural ismorphism between 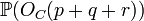 and the points in | KC | representing lines through the points s.
and the points in | KC | representing lines through the points s.
[edit] History and proofs
In 1857 Riemann proved the inequality 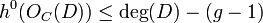 ; the proof used function theoretic methods on a gluing diagram of a 4g-gon. In 1865 Riemann's student Roch identified the difference in the inequality as the dimension of the cohomology group of differentials with prescribed zeros given by H0(OC(K − D)). In the second half of the 19th century, and in the beginning of the 20th century, a huge effort went into making the proof more geometric, and later more algebraic. (i.e. to get a proof over function fields which is independent of the geometric model). The problem in "geometrizing" the theorem is that in the 19th century, curves would always arise as embedded curves in some ambient projective space, and one had to find birationaly invariant definitions for the cohomology groups involved in the theorem. The problem in "algebraizing" the theorem is that one has to define differentials over function fields. In subsequent years the analytic, geometric and algebraic proofs have all been considerably simplified - we list references below. The current "standard" proof is the sheaf theoretic one: using modern tools, the theorem is an immediate consequence of Serre's duality, and the fact that if D,D' are divisors on C then χ(OC(D + D')) = χ(OC(D)) + χ(OC(D')).
; the proof used function theoretic methods on a gluing diagram of a 4g-gon. In 1865 Riemann's student Roch identified the difference in the inequality as the dimension of the cohomology group of differentials with prescribed zeros given by H0(OC(K − D)). In the second half of the 19th century, and in the beginning of the 20th century, a huge effort went into making the proof more geometric, and later more algebraic. (i.e. to get a proof over function fields which is independent of the geometric model). The problem in "geometrizing" the theorem is that in the 19th century, curves would always arise as embedded curves in some ambient projective space, and one had to find birationaly invariant definitions for the cohomology groups involved in the theorem. The problem in "algebraizing" the theorem is that one has to define differentials over function fields. In subsequent years the analytic, geometric and algebraic proofs have all been considerably simplified - we list references below. The current "standard" proof is the sheaf theoretic one: using modern tools, the theorem is an immediate consequence of Serre's duality, and the fact that if D,D' are divisors on C then χ(OC(D + D')) = χ(OC(D)) + χ(OC(D')).
[edit] Generalizations
The generalizations of the Riemann-Roch theorem come in two flavors: One direction views the Riemann-Roch theorem as a tool to study any linear system on a any curve. Clifford's theorem gives a better bound on the dimension of special linear systems on curve. If the assumption on the curve is relaxed to be a generic curve, then the Brill-Noether Theorem and the Petri Theorem give good descriptions of the geometry of the linear system.
Another direction of generalization, with more far-reaching consequences, is to view Riemann-Roch as a tool to compute the Euler characteristic of a vector bundle on a Variety. The first generalizations in this direction go back to the beginning of the 20th century with Riemann-Roch for surfaces and Noether's formula on surfaces. The next step, taken during the 1960s, is the Hirzebruch-Riemann-Roch theorem, which analyze the Euler characteristic of the canonical bundle of an arbitrary. The final step in the algebro-geometric setting is the Grothendieck-Riemann-Roch theorem, which analyzes the behaviour of the Euler characteristic of vector bundles under pullbacks; e.g. the Riemann-Roch theorem can be deduced from the Grothendieck-Riemann Roch theorem by projecting a curve to a point. In the analytic setting Grothendieck Riemann Roch had one more generalization: the Atiyah-Singer index theorem.
[edit] References
- J. Gray The Riemann-Roch theorem and Geometry Documenta Mathematica Extra Vo. ICM 1998 III 811-822, available online at [1] (history)
- E. Arabarello M. Cornalba P. Griffiths and J. Harris Geometry of Algebraic Curves: Volume 1 ISBN 0387909974 (classical geometric proof, many applications and examples)
- P. Grifiths and J. Harris Principles of Algebraic geometry ISBN 0-471-05059-8 Chapter 2.3 (analytic approach and sheaf theoretic approach, many applications and examples)
- M. Rosen Number theory in Function Fields ISBN 0-387-95335-3 Chapter 6 (algebraic approach)
- W. Fulton Intersection Theory ISBN 0387985492 Chapters 15 and 18 (sheaf theoretic approach and generalizations)
| |
Some content on this page may previously have appeared on Citizendium. |