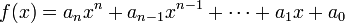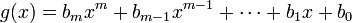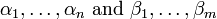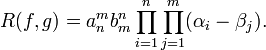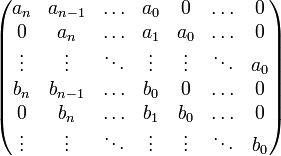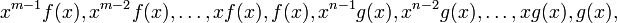Resultant (algebra)
In algebra, the resultant of two polynomials is a quantity which determines whether or not they have a factor in common.
Given polynomials
and
with roots
respectively, the resultant R(f,g) is defined as
The resultant is thus zero if and only if f and g have a common root.
[edit] Sylvester matrix
The Sylvester matrix attached to f and g is the square (m+n)×(m+n) matrix
in which the coefficients of f occupy m rows and those of g occupy n rows.
The determinant of the Sylvester matrix is the resultant of f and g.
The rows of the Sylvester matrix may be interpreted as the coefficients of the polynomials
and expanding the determinant we see that
- R(f,g) = a(x)f(x) + b(x)g(x)
with a and b polynomials of degree at most m-1 and n-1 respectively, and R a constant (degree zero polynomial). If f and g have a polynomial common factor this must divide R and so R must be zero. Conversely if R is zero, then f/g = - b/a so f/g is not in lowest terms and f and g have a common factor.
[edit] References
- J.W.S. Cassels (1991). Lectures on Elliptic Curves. Cambridge University Press. ISBN 0-521-42530-1. Chapter 16.
- Serge Lang (1993). Algebra, 3rd ed. Addison-Wesley, 200-204. ISBN 0-201-55540-9.
| |
Some content on this page may previously have appeared on Citizendium. |