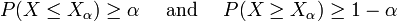Quantile
Quantiles are statistical parameters that divide the range of a random variable into two parts — values less than it and values greater than it — according to a given probability.
More precisely, an α-quantile is a real number Xα such that the random variable is less or equal to it with probability at least α, and greater or equal to it with probability at least (1–α). It is not possible to require equality because the probability of the value Xα may be positive. On the other hand, Xα may not be uniquely determined because of gaps in the range of the random variable.
In descriptive statistics, some frequently used quantiles have names of their own:
An α-quantile is
- a median for α = 0.5
- a (first) quartile for α = 0.25 and a third quartile for α = 0.75
- a kth quintile for
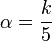
- a kth decile for
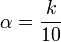
- a kth percentile for
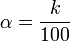
Moreover, for statistical tests the critical values (used to determine whether a result is significant or not) are quantiles of the test statistic.
[edit] Definition
For a real random variable X and a real number α (0 < α < 1), a real number Xα is an α-quantile if and only if
Remark: At least one of the inequalities is strict if P(X = Xα) > 0. and equality holds in both cases if P(X = Xα) = 0.
[edit] Quantiles and the distribution function
Essentially, quantiles are the values of the inverse function to
the (cumulative) distribution function, defined as 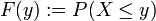 ,
with two exceptions:
,
with two exceptions:
- F is increasing, but not necessarily strictly increasing. There may be (at most countably many) values of α for which the F − 1({α}) is an interval (rather than a single number). In this case every element of that interval is an α-quantile. (For all values in the interior of the interval equality holds in both cases).
- The range of F may have (at most countably many) gaps (corresponding to discontinuities of F). For values of α in one of these gaps F − 1({α}) is empty, but the quantile exists (and is unique). (These gaps correspond to those values Xα that occur with positive probability.)
| |
Some content on this page may previously have appeared on Citizendium. |