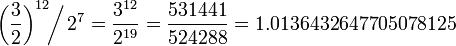Pythagorean comma
A Pythagorean comma is a microtonal musical interval, named after the ancient mathematician and philosopher Pythagoras. It is sometimes called a ditonic comma.
A comma is a very small musical interval between a note formed by one cycle of just intervals and the same note formed by another cycle of different just intervals. When ascending from an initial (low) pitch by a cycle of justly tuned perfect fifths (ratio 3:2), leapfrogging twelve times, one eventually reaches a pitch approximately seven whole octaves above the starting pitch. If this pitch is then lowered precisely seven octaves, the resulting pitch is (a very small amount over) 23.46 cents higher than the initial pitch. This microtonal interval is a Pythagorean comma:
That is, twelve perfect fifths are not exactly equal to seven perfect octaves, and the Pythagorean comma is the amount of the discrepancy.
This interval has serious implications for the various tuning schemes of the chromatic scale, because in Western music, twelve perfect fifths and seven octaves are treated as the same interval. Equal temperament, today the most common tuning system used in the West, accomplished this by flattening each fifth by a twelfth of a Pythagorean comma (two cents), thus giving perfect octaves.
[edit] History
Despite its name, the Pythagorean comma was first described in the West by pseudo-Euclid in Divisions of the Canon (c. 300 BCE). Chinese mathematicians were aware of the Pythagorean comma as early as 122 BCE (its calculation is detailed in the Huainanzi), and in about 50 BCE Ching Fang discovered that if the cycle of perfect fifths was continued beyond twelve all the way to fifty-three, the difference between this fifty-third pitch and the starting pitch would be much smaller than the Pythagorean comma; this difference was later named "Mercator's comma".
The standard epimoric approximation to the Pythagorean comma is the ratio 74:73; older works on tuning (before about 1970) often define the Pythagorean comma as the 74:73 ratio without mentioning that it is an approximation, especially in German works c.1850–1950. For example Hermann von Helmholtz, in his On the Sensations of Tone, uses 74:73 as the ratio of the Pythagorean comma (though he mentions once that it is only an approximation).
Other intervals of a similar size are the syntonic comma and the Holdrian comma.
[edit] Reading
- Hermann von Helmholtz On the Sensations of Tone as a Physiological Basis for the Theory of Music (translated with the author's sanction from the 3rd German edition, with additional notes and an additional appendix, by Alexander J. Ellis). London: Longmans, Green, & Co., 1875. Reprinted as On the Sensations of Tone (with a new introduction by H. Margenau). New York: Dover Publications, 1954. ISBN 0486607534
[edit] External links
- Tonalsoft Encyclopaedia of Tuning
- "The Pythagorean Circle" from Brian Capleton's "Music, Mathematics, Philosophy, and Tuning: Harmonic Theory Pages"
- "Pythagorean Comma" — Phil Sloffer
- "The 'Pythagorean Comma'" — Jody Nagel
| |
Some content on this page may previously have appeared on Citizendium. |