Pseudoprime
A pseudoprime is a composite number that has certain properties in common with prime numbers.
[edit] Introduction
To find out if a given number is a prime number, one can test it for properties that all prime numbers share. One property of a prime number is that it is only divisible by one and itself. This is a defining property: it holds for all primes and no other numbers.
However, other properties hold for all primes and also some other numbers. For instance, every prime number greater than 3 has the form 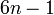 or
or 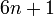 (with n an integer), but there are also composite numbers of this form: 25, 35, 49, 55, 65, 77, 85, 91, … . So, we can say that 25, 35, 49, 55, 65, 77, 85, 91, … are pseudoprimes with respect to the property of being of the form
(with n an integer), but there are also composite numbers of this form: 25, 35, 49, 55, 65, 77, 85, 91, … . So, we can say that 25, 35, 49, 55, 65, 77, 85, 91, … are pseudoprimes with respect to the property of being of the form 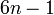 or
or 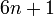 . There exist better properties, which lead to special pseudoprimes, as outlined below.
. There exist better properties, which lead to special pseudoprimes, as outlined below.
[edit] Different kinds of pseudoprimes
| Property | kind of pseudoprime |
|---|---|
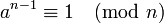 |
Fermat pseudoprime |
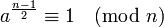
|
Euler pseudoprime |
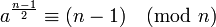
| |
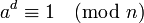
|
strong pseudoprime |
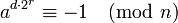
| |
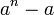 is divisible by is divisible by 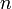 |
Carmichael number |
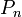 is divisible by is divisible by 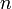 |
Perrin pseudoprime |
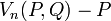 is divisible by is divisible by 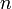
|
[edit] Table of smallest Pseudoprimes
| smallest Pseudoprimes | ||
|---|---|---|
| Number | Kind of Pseudoprime | Bases |
| 15 | Fermat pseudoprime | 4, 11 |
| 21 | Euler pseudoprime | 8, 13 |
| 49 | strong pseudoprime | 18, 19, 30, 31 |
| 561 | Carmichael number | |
| 1729 | absolute Euler pseudoprime | |
| |
Some content on this page may previously have appeared on Citizendium. |
