Primitive root
In number theory, a primitive root of a modulus is a number whose powers run through all the residue classes coprime to the modulus. This may be expressed by saying that n has a primitive root if the multiplicative group modulo n is cyclic, and the primitive root is a generator, having an order equal to Euler's totient function φ(n). Another way of saying that n has a primitive root is that the value of Carmichael's lambda function, λ(n) is equal to φ(n).
The numbers which possess a primitive root are:
- 2 and 4;
- pn and 2pn where p is an odd prime.
If g is a primitive root modulo an odd prime p, then one of g and g+p is a primitive root modulo p2 and indeed modulo pn for all n.
There is no known fast method for determining a primitive root modulo p, if one exists. It is known that the smallest primitive root modulo p is of the order of 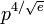 by a result of Burgess[1], and if the generalised Riemann hypothesis is true, this can be improved to an upper bound of 2(logp)2 by a result of Bach[2].
by a result of Burgess[1], and if the generalised Riemann hypothesis is true, this can be improved to an upper bound of 2(logp)2 by a result of Bach[2].
[edit] Artin's conjecture
Artin's conjecture for primitive roots states that any number g which is not a perfect square is infinitely often a primitive root. Roger Heath-Brown has shown that there are at most two exceptional prime numbers a for which Artin's conjecture fails.[3]
[edit] See also
[edit] References
- ↑ D.A. Burgess (1957). "The distribution of quadratic residues and non-residues". Mathematika 4: 106-112.
- ↑ Eric Bach (1990). "Explicit bounds for primality testing and related problems". Math. Comp. 55: 355--380.
- ↑ D.R. Heath-Brown (1986). "Artin's conjecture for primitive roots". Q. J. Math., Oxf. II. Ser. 37: 27-38.
| |
Some content on this page may previously have appeared on Citizendium. |
