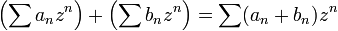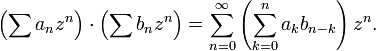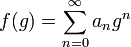Power series
In mathematics, a power series is an infinite series whose terms involve successive powers of a variable, typically with real or complex coefficients. If the series converges, its value determines a function of the variable involved. Conversely, given a function it may be possible to form a power series from successive derivatives of the function: this Taylor series is then a power series in its own right.
Formally, let z be a variable and an be a sequence of real or complex coefficients. The associated power series is
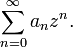 .
.
Contents |
[edit] Radius of convergence
Over the complex numbers the series will have a radius of convergence R, a real number with the property
that the series converges for all complex numbers z with 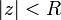 and that R is the "largest" number with this property (supremum of all numbers with this property. If the series converges for all complex numbers, we formally say that the radius of convergence is infinite.
and that R is the "largest" number with this property (supremum of all numbers with this property. If the series converges for all complex numbers, we formally say that the radius of convergence is infinite.
For example
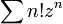 converges only for z = 0 and has radius of convergence zero.
converges only for z = 0 and has radius of convergence zero.
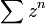 converges for all
converges for all 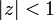 , but diverges for z = 1 and so has radius of convergence 1.
, but diverges for z = 1 and so has radius of convergence 1.
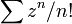 converges for all complex numbers z and so has radius of convergence infinity.
converges for all complex numbers z and so has radius of convergence infinity.
More generally we may consider power series in a complex variable z − a for a fixed complex number a.
Within the radius of convergence, a power series determines an analytic function of z. Derivatives of all orders exist, and the Taylor series exists and is equal to the original power series.
[edit] Convergence tests
Some of the standard test for convergence of series translate into computations of the radius of convergence R.
- D'Alembert ratio test: if the limit of the sequence
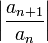 exists, then this is equal to 1/R.
exists, then this is equal to 1/R.
- Cauchy n-th root test: if the limit of the sequence
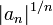 exists, then this is equal to 1/R.
exists, then this is equal to 1/R.
[edit] Algebra of power series
Power series may be added and multiplied. If 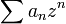 and
and 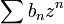 are power series, we may define their sum and product
are power series, we may define their sum and product
and these purely algebraic definitions are consistent with the values achieved within the region of convergence.
If a power series g has constant term b0 = 0, then the n-th power of g involves only powers of z with exponent at least n. Hence if f denotes the series 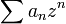 it makes sense to consider the composite
it makes sense to consider the composite
as a power series in z, since any given power of z will appear in only finitely many of the terms gn. Again this purely algebraic definition is consistent with function composition within the region of convergence.
[edit] Formal power series
Let R be any ring. A formal power series over R, with variable X is a formal sum 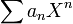 with coefficients
with coefficients 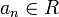 . Addition and multiplication are now defined purely formally, with no questions of convergence, by the formulae above. The formal power series form another ring denoted R[[X]].
. Addition and multiplication are now defined purely formally, with no questions of convergence, by the formulae above. The formal power series form another ring denoted R[[X]].
[edit] Inversion of power series
The power series f is called inverse series of the power series g, iff all elements of the expansion of f(g(z)) − z with respect to z are zero.
To simplify formulas, it is assumed that the zero-th element is zero, and the first coefficient is unity: f0 = 0, and f1 = 1. Then g0 = 0, and g1 = 1, and
- g2 = − f2
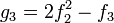
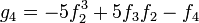
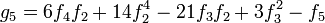
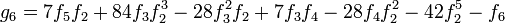
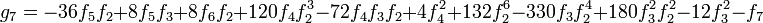
and so on.
| |
Some content on this page may previously have appeared on Citizendium. |