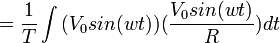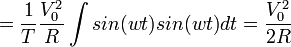Power (physics)
In physics, power is the rate of producing or consuming energy. It is also the rate of doing work. The watt (W), named after the Scottish engineer James Watt), is the SI unit for power and is defined as 1 Joule/second. Many products are rated by their ability to generate or use power. Household lightbulbs are usually rated in the 40-120 W range, as are many stereo systems. In the automotive industry, power is often expressed in units of horsepower, which is equivalent to 746 W or 550 ft•lbf/sec.
[edit] Electrical power
In direct current (DC) electronic circuits, in which a current I is flowing through a resistor R, and experiencing a voltage drop V, the power consumption can be expressed as I2R, VI or V2/R.
Calculating the power of AC circuits is more complex because both the voltage and the current are a function of time.
Given a sinusoidal time-dependent voltage, v(t) = V0sin(wt), or current i(t)= V0sin(wt)/R = I0sin(wt), the instaneous power p(t) at any time is given by:
Instantaneous AC power: p(t) = I02Rsin2(wt).
The instantaneous power is of little use in most applications, so AC power is usually represented as a power averaged over time.
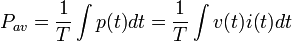
Since for a sinusoidal voltage, the rooot-mean-square power, Vrms is defined as
![V_{rms} = [\frac{1}{T}\int{v(t)v(t)dt}]^{1/2} = \frac{V_0}{\sqrt2}](../w/images/math/d/b/c/dbc908f31470075813d1fcf6c00ba1b1.png) , the average power can be rewritten as
, the average power can be rewritten as
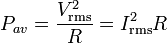
The root-mean-squared voltage is the value typically thought of in regular usage. Thus, in the U.S., standard 110 voltage lines refer to the Vrms value. The actual peak voltage is around 156 volts but it, and the Vrms actually vary throughout the day depending on electrical demand and sometime they fall low enough to cause a brownout.
| |
Some content on this page may previously have appeared on Citizendium. |