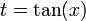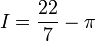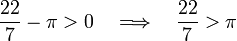Pi (mathematical constant)/Proofs/Student level proof that 22 over 7 exceeds Pi
From Knowino
We work out the following integral:
It is possible to divide polynomials in a manner that is analogous to long division of decimal numbers. By doing this it, can be shown that
where −4 is the remainder of the polynomial division.
Using:
for n=6, 5, 4, 2, and 0, respectively, one obtains
The following holds
The latter integral is easily evaluated by making the substitution
Hence
The integrand (expression under the integral) of the integral in equation (1) is everywhere positive on the integration interval [0, 1] and, remembering that an integral can be defined as a sum of integrand values, it follows that 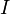 is positive. Finally,
is positive. Finally,
which was to be proved.


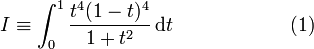
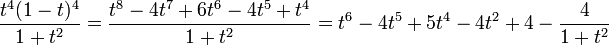
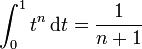
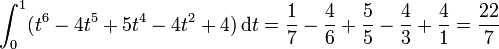
![-4\int_0^1 \frac{1}{1+t^2} \, \mathrm{d}t = -4\left[ \arctan(t) \right]^1_0 = -4\frac{\pi}{4} = -\pi](../../../w/images/math/c/6/f/c6f3789e29e5f7f040a8f16bf38dbe8a.png)